Предмет: Алгебра,
автор: user2682
найдите первообразную
Приложения:
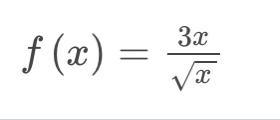
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Избавимся от иррациональности в знаменателе:
Найдём первообразную:
__________________
Задание решено по следущей формуле первообразной:
Похожие вопросы
Предмет: Русский язык,
автор: Mafia7845
Предмет: Русский язык,
автор: амир1110
Предмет: Английский язык,
автор: александра2101
Предмет: Математика,
автор: den989488
Предмет: Английский язык,
автор: layemaxaw