Допоможіть будь ласка
Які з данних функцій є зростаючими?
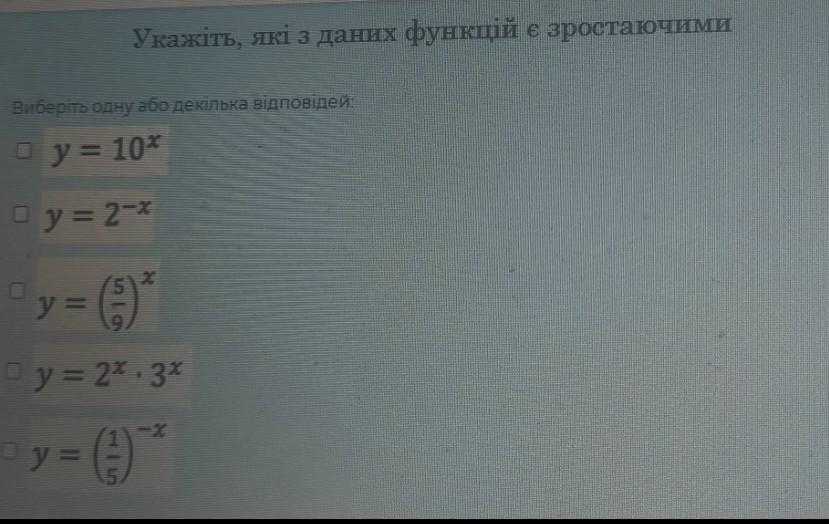
Ответы
Ответ:
Функции у=10ˣ; у=2ˣ * 3ˣ и у=(1/5)⁻ˣ возрастающие на множестве всех действительных чисел.
Объяснение:
Показательная функция вида y=aˣ является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 < a < 1.
Приводим каждую из функций к виду y=aˣ и сравниваем основание а с единицей.
Основание а=10, 10>1 ⇒ функция у=10ˣ возрастающая на множестве всех действительных чисел.
Применяем свойство степеней a⁻ᵇ = 1/aᵇ.
Основание а=1/2, 1/2<1 ⇒ функция у=2⁻ˣ убывающая на множестве всех действительных чисел.
Основание а=5/9, 5/9<1 ⇒ функция у=(5/9)ˣ убывающая на множестве всех действительных чисел.
Применяем свойство степеней aˣ * bˣ = (ab)ˣ.
Основание а=6, 6>1 ⇒ функция у=2ˣ * 3ˣ возрастающая на множестве всех действительных чисел.
Применяем свойство степеней a⁻ᵇ = 1/aᵇ.
Основание а=5, 5>1 ⇒ функция у=(1/5)⁻ˣ возрастающая на множестве всех действительных чисел.