Предмет: Математика,
автор: petr018
Найти производную ....
Приложения:
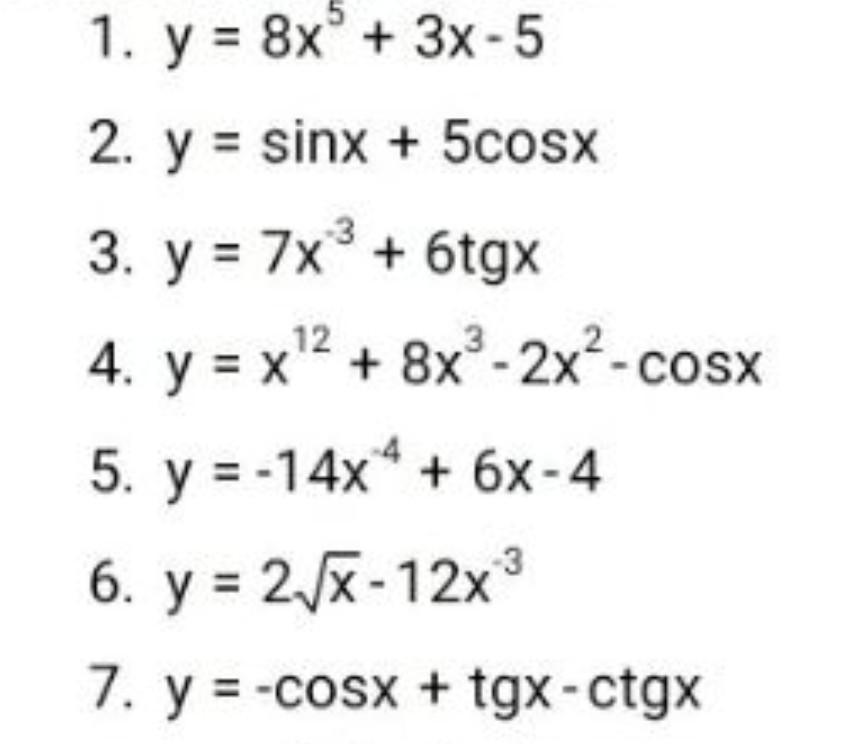
Ответы
Автор ответа:
2
Ответ:
решение смотри на фотографии
Приложения:


Автор ответа:
2
Ответ:
1.
2.
3.
4.
5.
6.
7.
Пошаговое объяснение:
Найти производную.
Надо знать формулы:
1.
2.
3.
4.
5.
6.
7.
Похожие вопросы
Предмет: Русский язык,
автор: natadeputat
Предмет: Українська мова,
автор: mirvoda72
Предмет: Українська література,
автор: olegeriy1
Предмет: Химия,
автор: foresd2003
Предмет: Биология,
автор: dasha2873