Предмет: Математика,
автор: makcnm1234
СРОЧНО!!! ДАЮ 100 БАЛЛОВ. Нужно решить уравнение и найти все корни, которые принадлежат промежутку {6pi;7pi} ПОЖАЛУЙСТА С ПОДРОБНЫМ ОВТЕТОМ!!
Приложения:
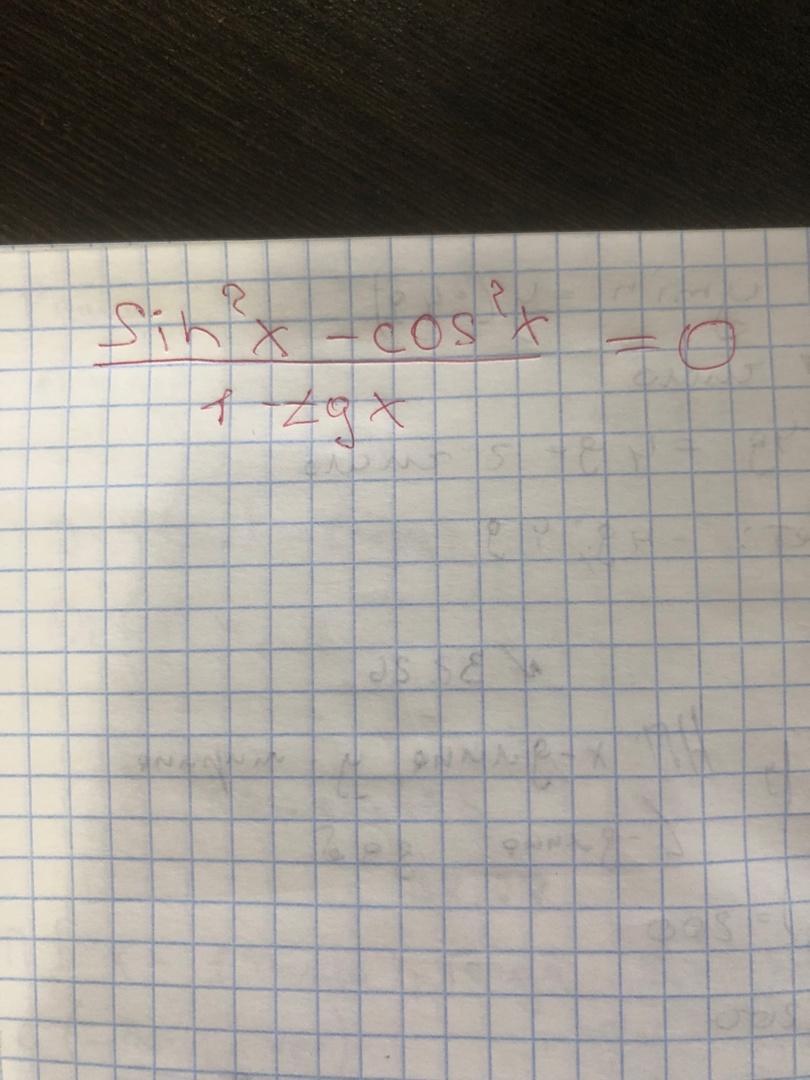
iiiof:
кррррп
Ответы
Автор ответа:
2
Ответ: Один корень
Пошаговое объяснение:
Находим корни которые принадлежат промежутку [6π ; 7π]
При n = 6
При n = 7
Просто лучший!!
Похожие вопросы
Предмет: Русский язык,
автор: arushambaryan1
Предмет: Қазақ тiлi,
автор: Сабина5851
Предмет: Другие предметы,
автор: майнкрафт23
Предмет: Математика,
автор: vladimirzholud13
Предмет: Информатика,
автор: ivanishcheva2005