Предмет: Алгебра,
автор: bumblephii
Помогите срочно пожалуйста
Приложения:
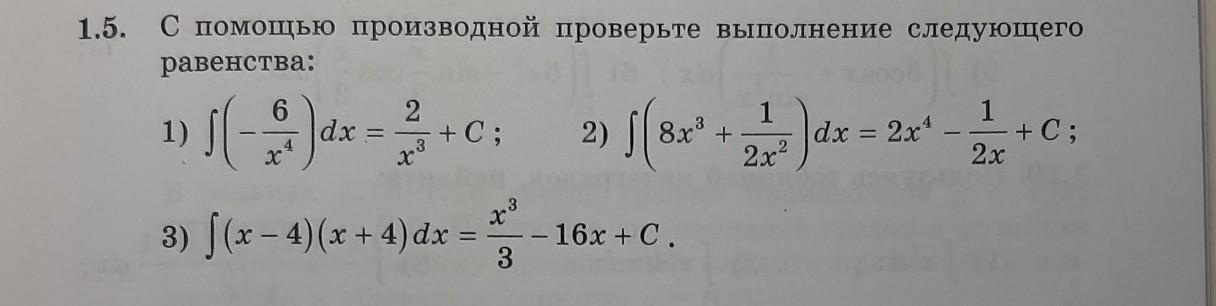
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Sasharus356
Предмет: Другие предметы,
автор: Marat651
Предмет: Українська мова,
автор: grilldom
Предмет: География,
автор: alina2212032003
Предмет: Математика,
автор: sashamatsiuk999