Question

$y = \sqrt{9 - {x}^{2} }$
Найти:
Область определения;
Область значения;
Знакопостоянство;
Нули;
С подробным пояснением.
​

Answer 1

Ответ:

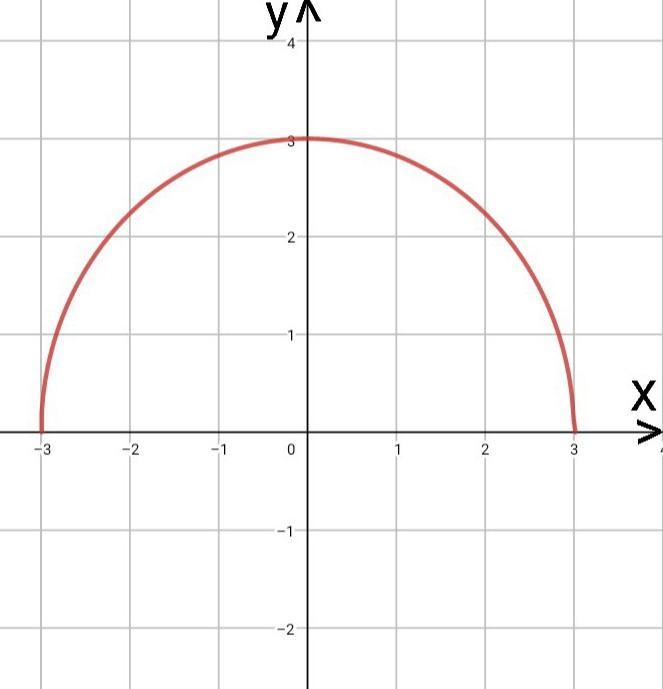
D(y)=[-3;3] , E(y)=[0,3] , у>0 на (-3;3) , Нули : ±3

Объяснение:

Область определения : Нужно найти все числа ,  которые может принимать х , но подкоренное выражение при этом ,должно иметь смысл , мы знаем , что подкоренное выражение не может быть отрицательным , значит , $9-x^2\geq 0$.

$9-x^2\geq 0\\-x^2\geq 0-9\\-x^2\geq -9\\x\leq \pm 3$

Поэтому ,  $D(y)=[-3;3]$.

Область значения : Теперь , из всевозможных значений х , нам нужно узнать , какому ,  наименьшему числу может равняться функция, но нужно одновременно учитывать  , что отрицательному числу функция равняться не может , т.к подкоренное выражение выдаст только положительные результаты , аналогично , что 0- это наименьшее число , которое может принимать у , т.к если взять из области определения число 3 или -3 ,  то $\sqrt{9-(\pm3)^2} =\sqrt{9-9} =0$  ,  а наибольшее значение это - "3" , т.к если взять из области определения число 0 , то $\sqrt{9-0^2} =\sqrt{9}=\pm 3$ , но из этого не может быть "-3" исходя из вышеуказанного объяснения ,  тогда $E(y)=[0;3]$.

Промежутки знакопостоянства : Если изобразить этот график на координатной оси , то опираясь на D(y) и E(y) мы выдим , что график будет напоминать полуокружность с радиусом R=3 , поэтому ,  $у > 0$ на промежутках $(-3;3)$ , а где $у < 0$ таких промежутков не существует.

Нули функции : Это точки оси Ох , где пересекается график , анологично , как мы уже нашли  , это  точки $x=\pm3$