помогите решить эти задания, хотя бы одно из них
матеша 10 класс дам 15 балов!!!!)
Ответы
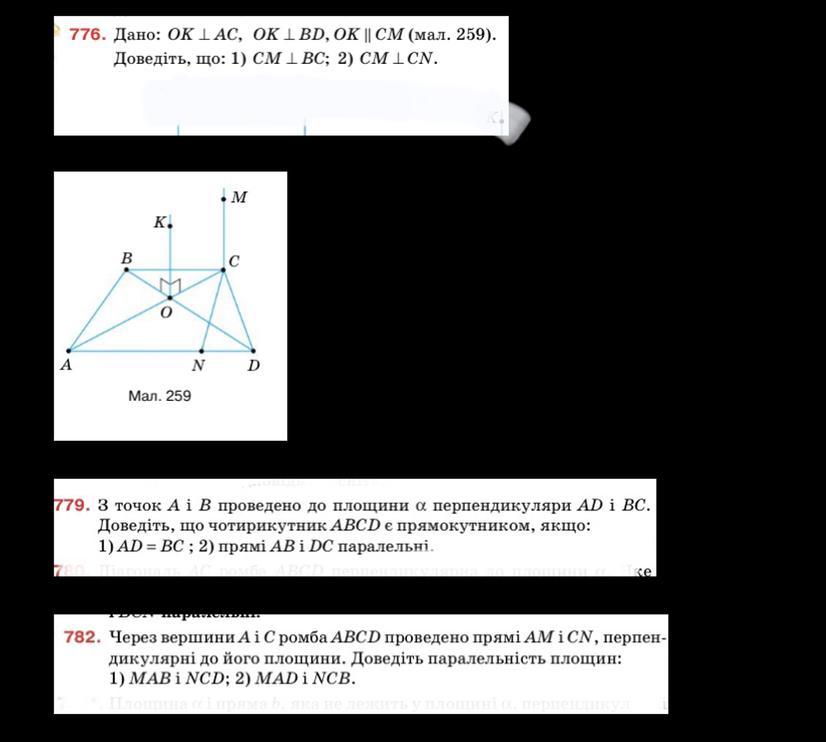
1) Якщо пряма паралельна до двох прямих, які лежать в одній площині і перетинаються, то вона перпендикулярна до даної площини.
І якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна до іншої.
Отже, за цьома двома властивостями можна стверджувати, що пряма СМ перпендикулярна до СN.
На малюнку видно, що фігура є трапецією, а її дві основи паралельні. Якщо опустити пряму СМ нище аж до перетину основи АД, то можна побачити, що вона створює прямокутний трикутник, а отже перепендикулярна до ВС.
2) В принципі умови доведення вже є поясненням.
У прямокутника:
-протилежні сторони паралельні
- кожен кут дорівнює 90 градусам.
З цих умов виконується як мінімум одна отже АБСД є прямокутником.
3) В задачі зауважили, що АМ і СN перпендикулярні до площини, а отже вони грають роль центральної точки, тобто перетин діагоналей ромба.
-Вертикальні кути рівні = 90 градусів
- Протилежні кути теж рівні, а в цьому випадку поділені навпіл прямою, що є бісектрисою
Всі ці факти тільки більше доводять, що трикутники ABM=NCD MAD=NCB.
Ці площини між собою мають спілку точку, а за вже відомою аксіомою: "Якщо дві площини мають спільну точку, то вони лежать на одній прямій". Що є доказом їхньої паралельності