Question

реши неравенство (z^2+1)(z^2-196)/z^2-9≥0

Answer 1

Ответ:

$z\in(-\infty;-14]\cup(-3;3)\cup[14;+\infty)$

Объяснение:

$\dfrac{(z^2+1)(z^2-196)}{z^2-9} \ge 0$

Решаем методом интервалов, сначала разложим на множители

$\dfrac{(z^2+1)(z+14)(z-14)}{(z-3)(z+3)} \ge 0$

Выражение $z^2+1$ для любого $z\in\mathbb{R}$ больше 0 и на знак не влияет

$\dfrac{(z+14)(z-14)}{(z-3)(z+3)} \ge 0$

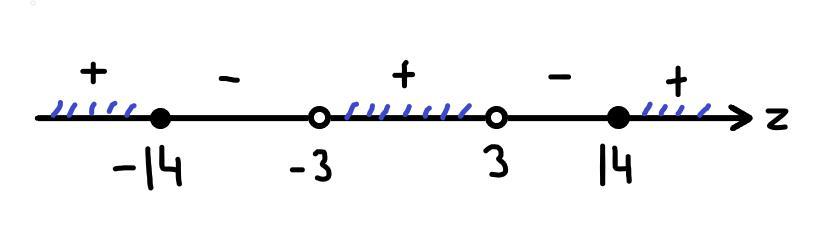
Раставим нули множителей, определим знаки. Так как неравенство не строгое, точки в числителе оставим закрашенными, а в знаменателе - выколотыми.

$z\in(-\infty;-14]\cup(-3;3)\cup[14;+\infty)$