Question

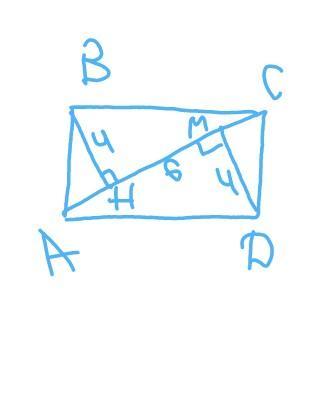
1. Из вершин противоположных углов прямо-
угольника к диагонали проведены перпенди-
куляры, расстояние между основаниями пер-
пендикуляров равно 6 см. Найти площад
прямоугольника, если длина перпендикуляра
равна 4 см. С рисунком пж

Answer 1

Объяснение:

ВН=DM=4см

НМ=6 см

из условия имеем прямоугольный треугольник АВС.

пусть АН=СМ=х см,тогда по свойству прямоугольных треугольников:

ВН²=АН×НС

НС=НМ+СМ=(6+х) см

4²=х×(6+х)

16=6х+х²

х²+6х-16=0

D=6²-4×1×(-16)=36+64=100

x1=(-6+10)/2=2 см

x2=(-6-10)/2= -8 не подходит

АН=СМ=2 см

АС=АН+НМ+СМ=2+6+2=10 см

S(ABCD)=AC×BH=10×4=40 cм²,т.к диагональ делит прямоугольник на два прямоугольных треугольника.

ответ: S(ABCD)=40 cм²