Предмет: Геометрия,
автор: valeriabler95
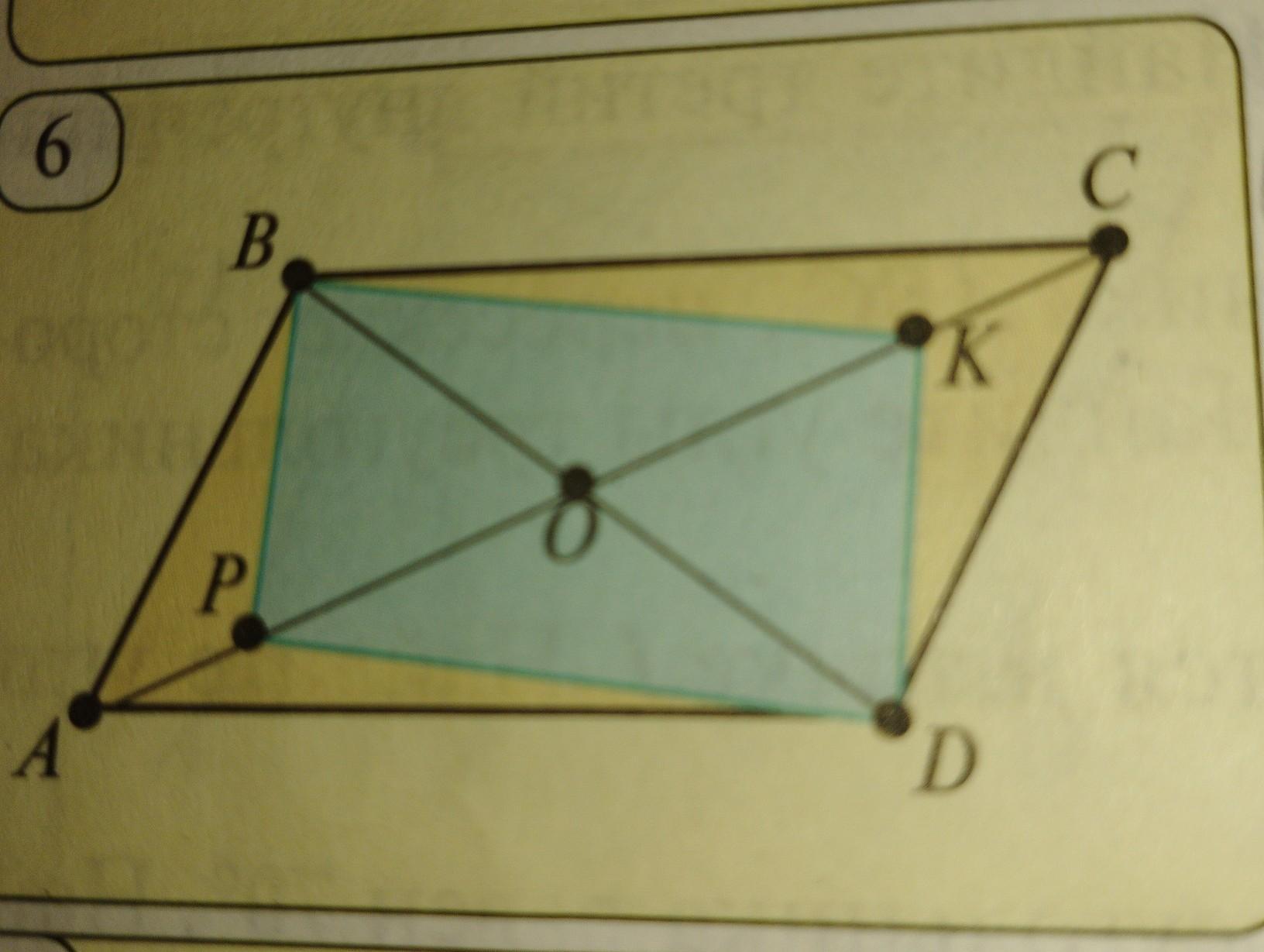
1.22. На большей диагонали АС параллелограмма ABCD выбраны точки Р и К (puc. 6). Докажите, что четырехугольник ВKDP-прямоугольник, если OP=OB=OK.
Приложения:
Ответы
Автор ответа:
1
Диагонали параллелограмма точкой пересечения делятся пополам (свойство параллелограмма).
ABCD - параллелограмм => OB=OD
Если диагонали четырехугольника равны и точкой пересечения делятся пополам, то четырехугольник является прямоугольником (признак прямоугольника).
OP=OK=OB=OD => BKDP - прямоугольник
valeriabler95:
спасибо большое))
Похожие вопросы
Предмет: Русский язык,
автор: трансформер3
Предмет: Окружающий мир,
автор: Булат114253576
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: Dilhan
Предмет: Русский язык,
автор: glebmgn