Предмет: Математика,
автор: nikofasolu
Помогите решить 9 класс алгебра даю 30 баллов
Тема
Функция. Область определения и область значений функции
Приложения:
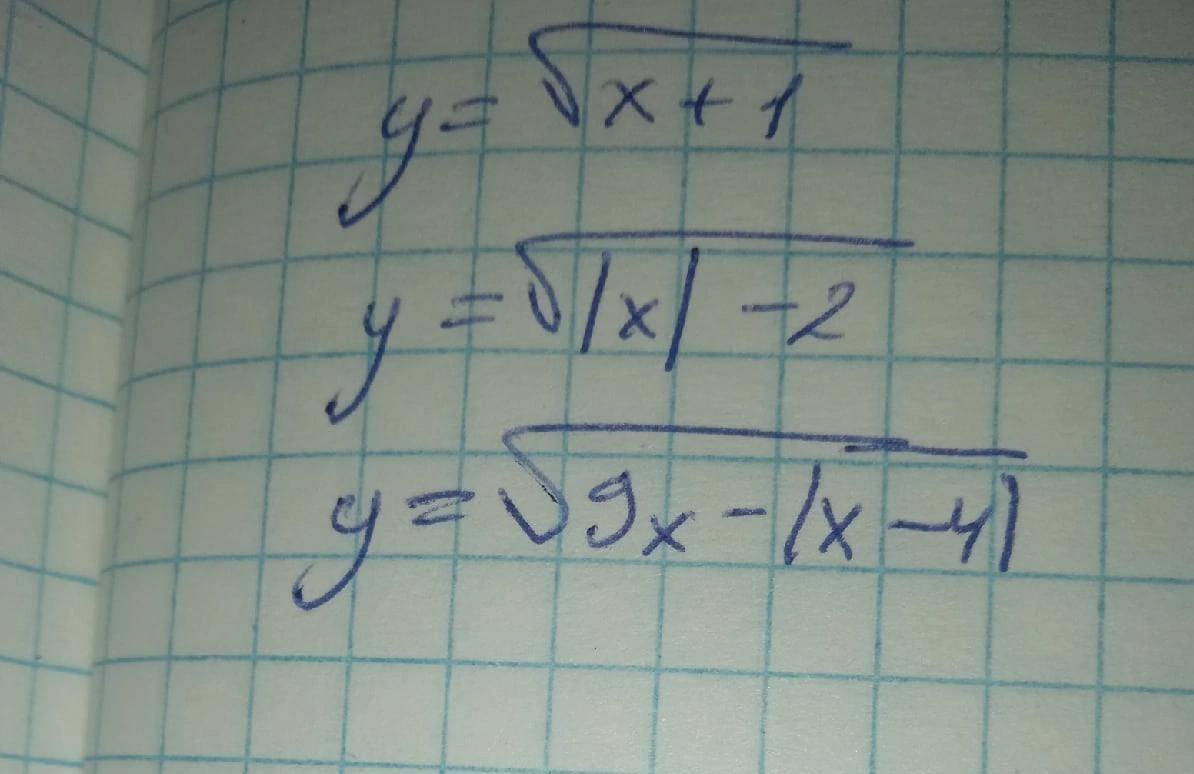
Ответы
Автор ответа:
0
Ответ:
1) [−1,+∞)
2) (−∞,−2]∪[2,+∞)
3) [2/5,+∞)
Автор ответа:
0
Відповідь:
Покрокове пояснення:
Область визначення D(f(x)) - множина аргументів, у яких функція має сенс, тобто. коли допустимі обчислення на речових числах.
Єдиним обмеження тут є арифметичний квадратний корінь, котрому в речових числах накладено заборону його вилучення з негативних чисел.
1)
2)
3)
Ясно, що , інакше таке неможливо,
Тоді або , або
,
з урахуванням вищесказаного:
Область значень E(f(x)) - множина значень (y), які приймає функція.
При
При
При
При
При
При
Так що:
Похожие вопросы
Предмет: Русский язык,
автор: borisenko27
Предмет: Українська мова,
автор: mariannagetsko
Предмет: Окружающий мир,
автор: kseniya52
Предмет: Русский язык,
автор: nadyasah2010
2) (−∞,−2]∪[2,+∞)
3) [2/5,+∞)