Предмет: Алгебра,
автор: yarik24012007
Найти действительные решения системы уравнения.
Приложения:
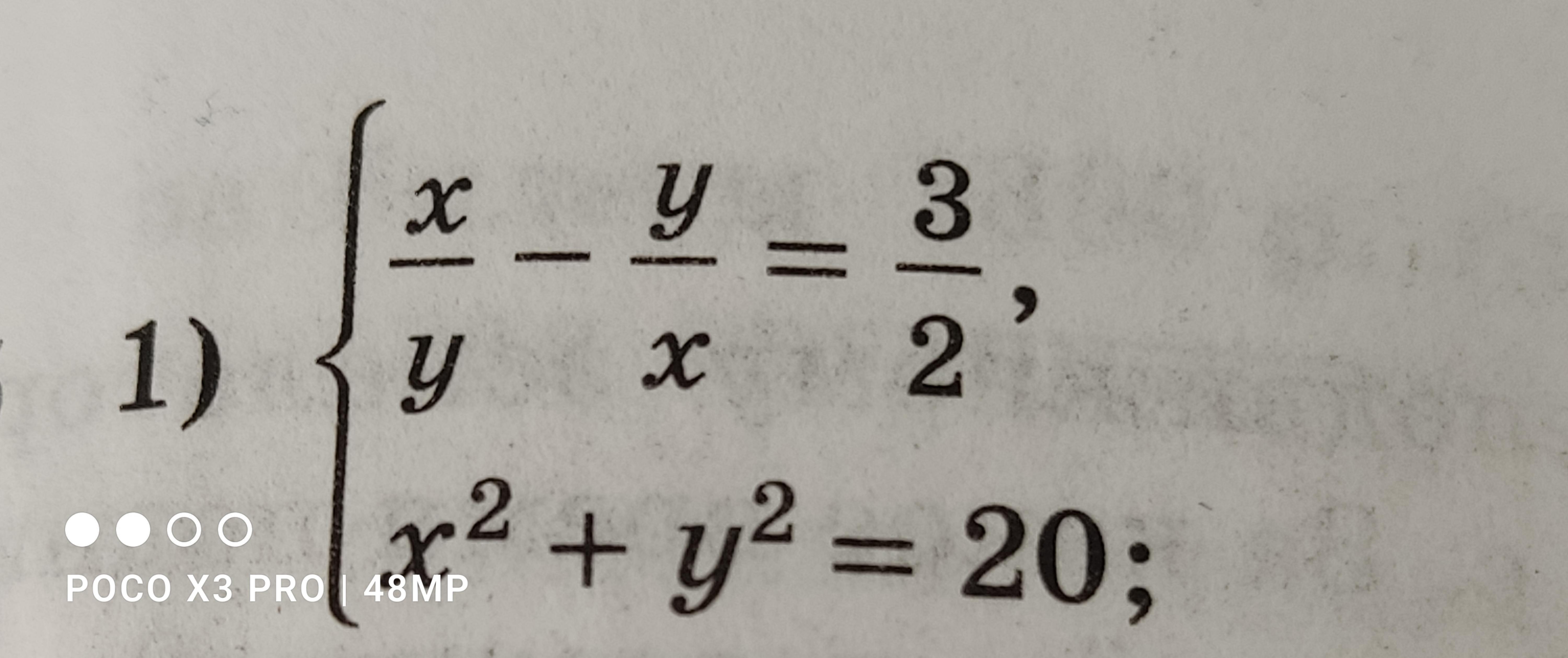
Ответы
Автор ответа:
1
Ответ:
(-4;-2), (4;2), (-2;4), (2;-4)
Объяснение:
Похожие вопросы
Предмет: Технология,
автор: Аноним
Предмет: Русский язык,
автор: щшнпек4у3ц
Предмет: Русский язык,
автор: graf2004
Предмет: Музыка,
автор: Sedaaa22