Предмет: Алгебра,
автор: allalemisko7
доведіть тотожность
Приложения:
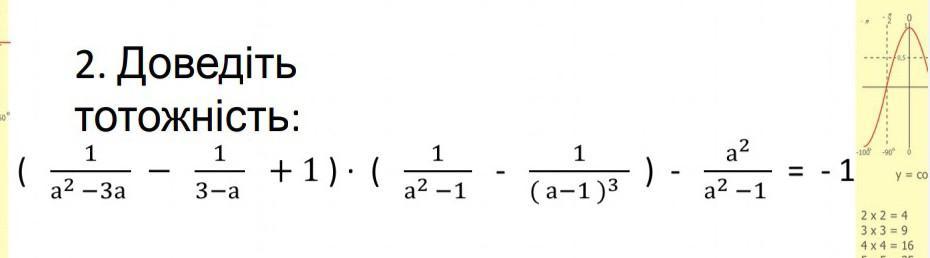
Ответы
Автор ответа:
3
Ответ:
Применяем формулы сокращённого умножения .
.
Тождество доказано .
Angelina598:
Здравствуйте,помогите пожалуйста с алгеброй
Похожие вопросы
Предмет: Английский язык,
автор: Aidemi55
Предмет: Окружающий мир,
автор: klevczova71
Предмет: Английский язык,
автор: itana1346
Предмет: Музыка,
автор: Sedaaa22