Предмет: Геометрия,
автор: polina753028
№ 3. Знайти косинус найменшого кута трикутника, сторони якого дорівнюють 5 см, 6 см, 9 см.
Ответы
Автор ответа:
1
Ответ:
Объяснение:
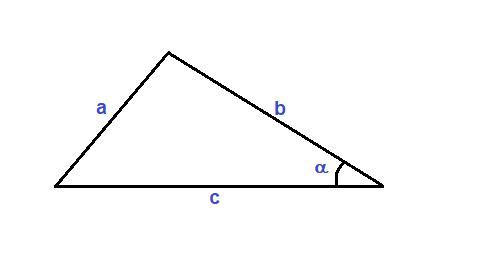
а = 5 см, b = 6 см, с = 9 см
В треугольнике против меньшей стороны лежит меньший угол. Значит, надо найти косинус угла α.
По теореме косинусов:
a² = b² + c² - 2bc · cos α
2bc · cos α = b² + c² - a²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Aлинa1
Предмет: Окружающий мир,
автор: Barb3452
Предмет: Математика,
автор: Maksat071107
Предмет: Математика,
автор: Krid533