Предмет: Математика,
автор: RuslanRussia1881
пожалуйста помогите математика 9 класс
Приложения:
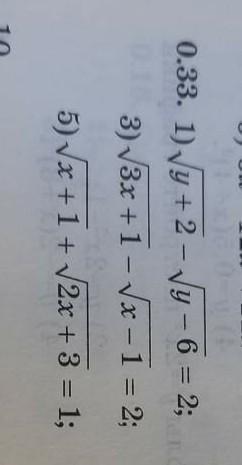
Ответы
Автор ответа:
0
Ответ:
1)√(y+2)=2+√(y-6)
y+2=4+4√(y-6)+y-6
√(y-6)=1
y-6=1
y=7
Дальше лень)
Автор ответа:
0
Ответ:
1) Ответ: 7.
3) Ответ: 1; 5.
5) Ответ: -1.
Пошаговое объяснение:
Решить уравнения:
- Подкоренное выражение неотрицательно.
ОДЗ: у ≥ -2 и у ≥ 6
⇒ у ≥ 6
Уединим корни. Перенесем один корень в правую часть и возведем в квадрат обе части:
Еще раз возведем обе части в квадрат:
Проверка:
Верно.
Ответ: 7.
ОДЗ: х ≥ -1/3; х ≥ 1
⇒ х ≥ 1
Делаем аналогично:
Еще раз возведем обе части в квадрат:
Проверка:
5:
Верно.
1:
Верно.
Ответ: 1; 5.
ОДЗ: х ≥ -1; х≥ -1,5
⇒ х ≥ -1
Проверка:
3:
⇒ 3 - посторонний корень.
-1:
Верно.
Ответ: -1.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: aizikonchik
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: IFMKMM0610
Предмет: История,
автор: otryvina19vika
Предмет: Русский язык,
автор: Аноним