Предмет: Геометрия,
автор: diankakorshunova30
срочно помогите пожалуйста
1. Внутри квадрата ABCD выбрана точка P так, чтобы треугольник BCP был равносторонним. На стороне BC выбрана точка Q такая, что AQB = PQC = a. Найдите меру угла а.
Ответы
Автор ответа:
3
Задачка простенькая, но очень известная и полезная. Обычно просят найти ∠PAB (ну или ∠PAD, кому как нравится), и по ходу я его тоже нахожу.
Для начала надо построить точку Q. Для этого надо отразить A симметрично относительно BC. Пусть это точка E. Точка Q лежит на пересечении BC и PE.
△APE прямоугольный, так как медиана BP в нем равна половине стороны AE. То есть AP ⊥ EP
Уже сейчас можно сказать, что требуемый к нахождению ∠PQC = ∠PAB; так как стороны этих углов попарно перпендикулярны.
Остается найти тот самый ∠PAB. Для этого надо заметить, что △APB равнобедренный, AB = BP, и ∠PBA = 30°; все это очевидно следует из того, что ABCD - квадрат, а △BPC правильный.
=> ∠PAB = (180° - 30°)/2 = 75° =∠PQC; ну и все.
Приложения:
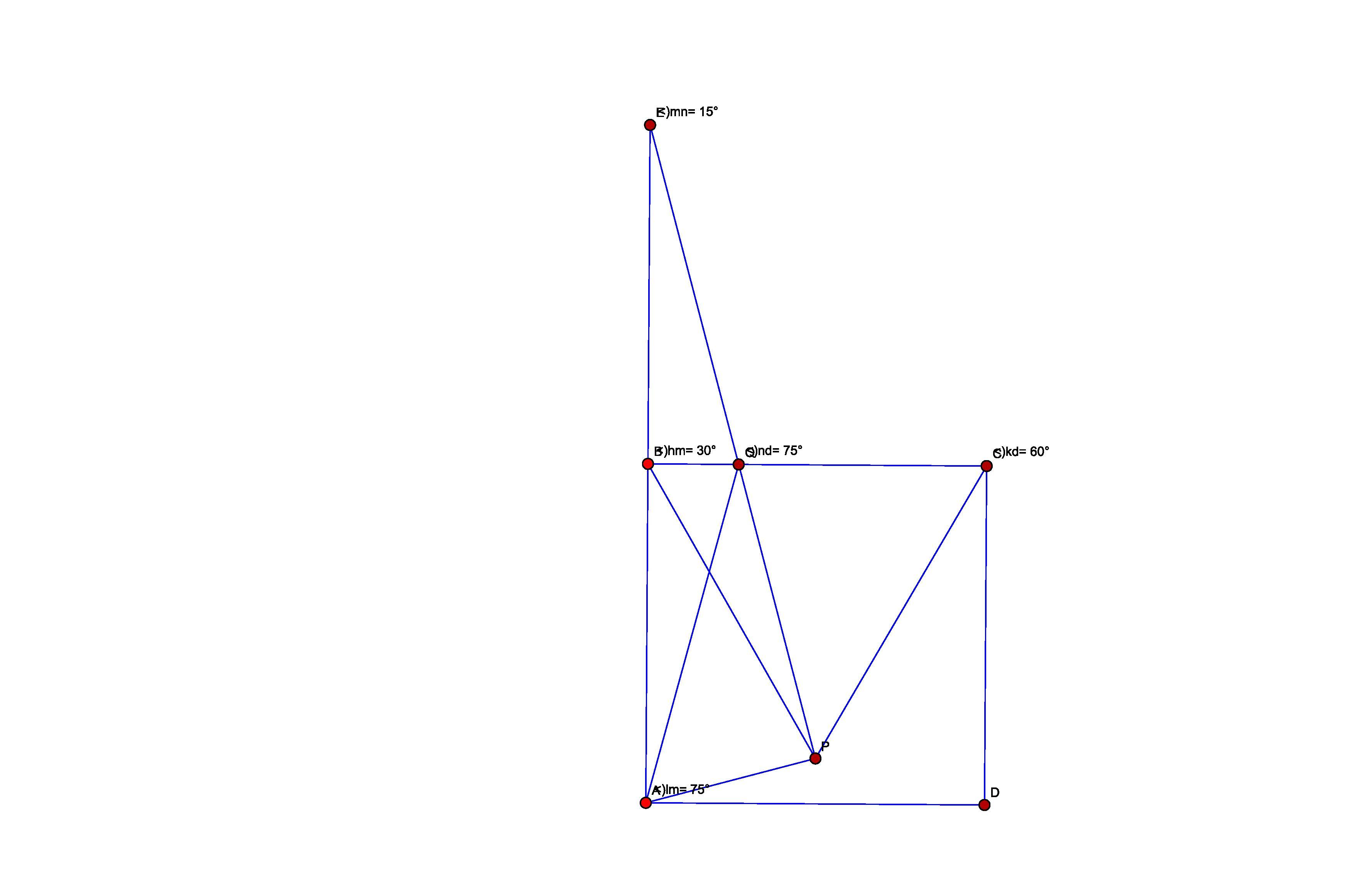
cos20093:
Чертеж получился "с мусором", но вроде все понятно. Интересно, что четырехугольник ABQP оказался вписанным (то есть все 4 точки лежат на одной окружности). В какой-то точке эта окружность пересекает CP. Докажите, что эта точка лежит на диагонали BD. Сможете - считаете, что вы все поняли :)
мне нравятся Ваши решения именно благодаря такому "мусору". Ваше мышление находится над уровнем обычных учебных. Не многим это по плечу, на этом сайте я знаю еще пару таких людей, поэтому всегда интересуюсь их и вашим решением....
Похожие вопросы
Предмет: Русский язык,
автор: Mshikhov
Предмет: Русский язык,
автор: 5058507
Предмет: Русский язык,
автор: КсенькаЛарионова1
Предмет: Информатика,
автор: vanyushaogorod