Предмет: Алгебра,
автор: rishatfakhredinov
4) 2 +4 a +3 2 + 1 a + 1 < 3 a + 2
Приложения:
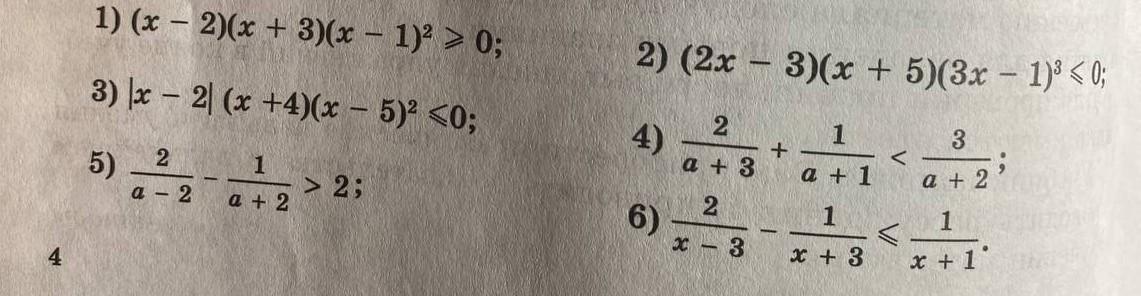
Ответы
Автор ответа:
1
Решим неравенство методом интервалов :
/////////////// //////////////// /////////////
Похожие вопросы
Предмет: Окружающий мир,
автор: Катякатя111111
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: p1nokoaldko
Предмет: Математика,
автор: lookk77
Предмет: Физика,
автор: missislera2006