Question

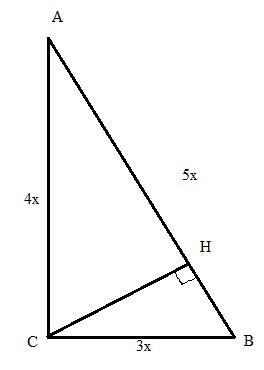
Дан прямоугольный треугольник. Высота опущена на гипотенузу и равна 24 сантиметра, стороны треугольника относятся как 3:4:5. Найдите периметр и площадь треугольника.

Answer 1

Ответ:

Р=120см, S=600см²

Объяснение:

Пусть СН=24см - высота, проведённая из вершины прямого угла прямоугольного треугольника АВС. Пусть х - 1 часть. Тогда стороны треугольника будут ВС=3х, АС=4х, АВ=5х.

Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

Расмотрим △АВС и △АСН. У них СН/ВС=АС/АВ или

24/3х=4х/5х

12х²=120х

х=0 или х=120/12=10см

Тогда АВ=5*10=50см, ВС=3*10=30см, АС=4*10=40см.

Р=АВ+ВС+АС=50+30+40=120см

S=1/2*АС*ВС=1/2*40*30=600см²