Предмет: Алгебра,
автор: maximchik009
ПОМОГИТЕ ПЖ!! Тригонометрическое уравнение
Приложения:
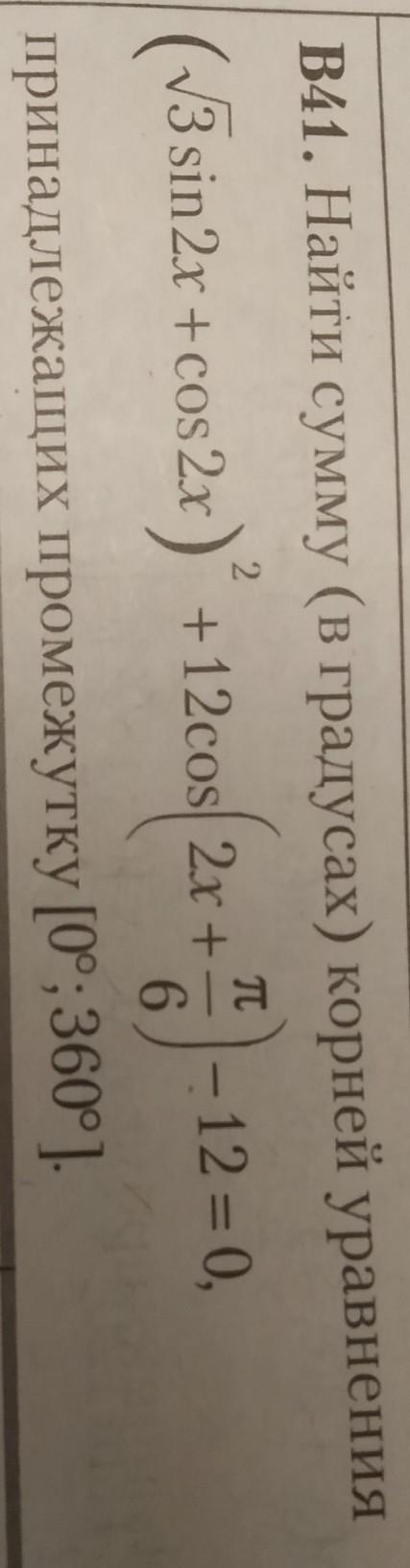
Ответы
Автор ответа:
1
Ответ:
Решить тригонометрическое уравнение .
Преобразуем выражение в скобках и воспользуемся формулой синуса суммы углов .
Промежутку принадлежат корни:
maximchik009:
Благодарю!
Можешь помочь с прошлым моим вопросом?
на которого нет ответа
Похожие вопросы
Предмет: Английский язык,
автор: Аня2301
Предмет: Русский язык,
автор: ооор3
Предмет: Окружающий мир,
автор: лвовлвжст
Предмет: Українська література,
автор: polinasemanik1
Предмет: История,
автор: liana152002