Question

ПРОШУ, ПОЖАЛУЙСТА, СРОЧНО!!!!!
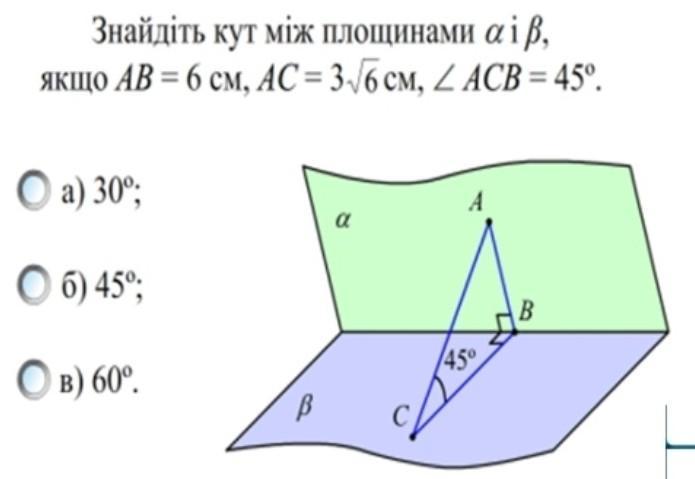
знайдіть кут між площинами альфа і бета , якщо AB=6 см, AC=3√6, кут ACB=45°​

Answer 1

Ответ:

Угол между плоскостями равен 60°.

Пошаговое объяснение:

Так как АВ и ВС - перпендикуляры к линии пересечения плоскостей, то ∠АВС - линейный угол двугранного угла между плоскостями, искомый.

Рассмотрим треугольник АВС:

по теореме синусов:

$\dfrac{AB}{\sin\angle ACB}=\dfrac{AC}{\sin\angle ABC}$

$\sin\angle ABC=\dfrac{AC\cdot\sin\angle ACB}{AB}$

$\sin\angle ABC=\dfrac{3\sqrt{6}\cdot \frac{\sqrt{2}}{2}}{6}=\dfrac{\sqrt{6}\cdot \sqrt{2}}{4}=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}$

∠ABC = 60°