Острые углы AuD равнобедренной трапеции ABCD равны 60' Отношение ее основ равно 3 Найдите значение угла BKC если CK высота трапеции
Ответы
Ответ:
∠ВКС=30°
Пошаговое объяснение:
Острые углы A и D равнобедренной трапеции ABCD равны 60°. Отношение ее основ равно 3. Найдите значение угла BKC если CK высота трапеции.
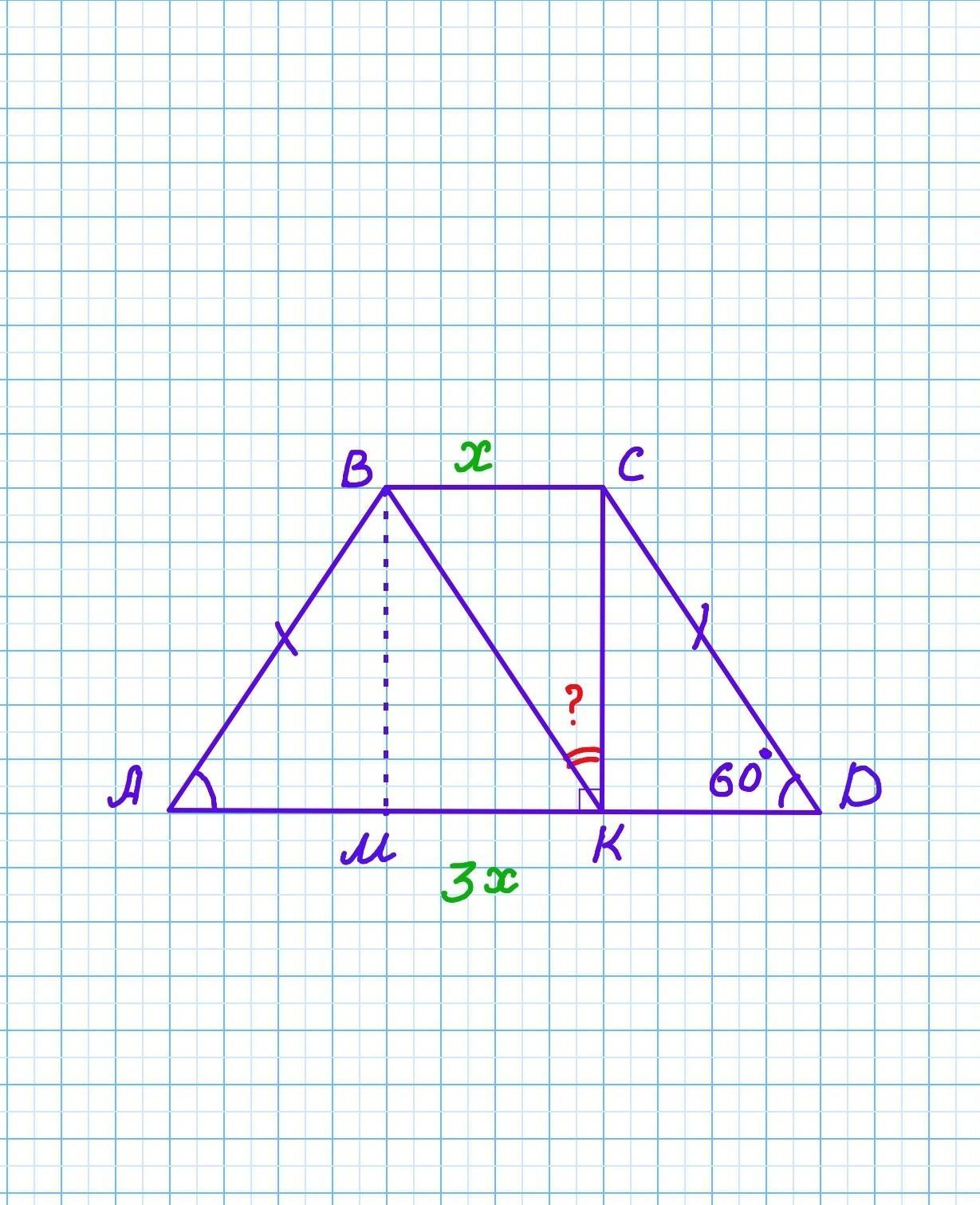
Дано: ABCD - трапеция. BC II AD, AB=CD, CK⟂AD, BC:AD=1:3. ∠A=∠D=60°.
Найти: ∠ВКС.
Пусть BC=x, тогда AD=3х.
Проведем высоту BM⟂AD. Поскольку трапеция равнобедренная, то △ABM=△DCK по гипотенузе и острому углу (AB=CD, ∠A=∠D).
Из равенства треугольников следует равенство сторон:
AM=KD=(AD-BC):2=(3х-х):2=2х:2= х
Рассмотрим четырёхугольник BCDK.
BC II KD - как основания трапеции, BC=KD=х.
- Если в четырёхугольнике две противоположные стороны равны и параллельны то этот четырёхугольник параллелограмм.
Следовательно BCDK - параллелограмм, а значит CD II BK.
∠BKC=∠DCK - как внутренние накрест лежащие углы при параллельных прямых CD и BK и секущей CK.
∠BKC =∠DCK=90°-∠D=90°-60°= 30° - так как сумма острых углов прямоугольного треугольника CDK(∠K=90°) равна 90°.