Question

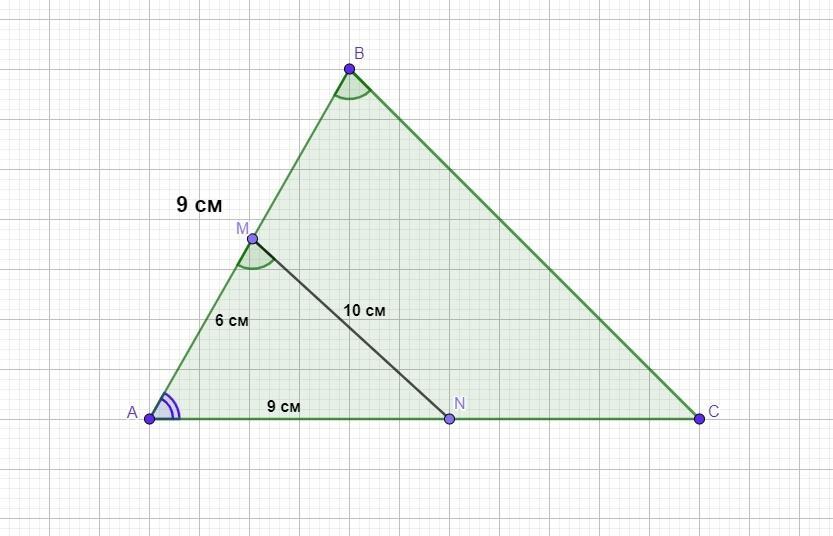
помогите пж У трикутнику ABC відомо, що АВ=9 см Через точку М сторони АВ проведено пряму, яка паралельна стороні ВС і перетинае сторону АС у точці N . Знайдіть невідомі сторони трикутника ABC якщо AM-6 см, MN=10 см, AN=9 CM

Answer 1

Ответ:

Невідомі сторони трикутника ABC: BC = 15 см, AC = 13,5 см

Пошаговое объяснение:

У трикутнику ABC відомо, що АВ=9 см. Через точку М сторони АВ проведено пряму, яка паралельна стороні ВС і перетинае сторону АС у точці N . Знайдіть невідомі сторони трикутника ABC якщо AM-6 см, MN=10 см, AN=9 см

Дано: ΔАВС, MN║BC, АВ=9 см, AM=6 см, MN=10 см, AN=9 см

Знайти: ВС, АС.

Розглянемо трикутники ABC і AMN: у них ∠A - спільний,  ∠ABC=∠AMN - як відповідні кути при паралельних прямих MN і BC та січній АВ.

Звіди випливає, що трикутники ABC і AMN подібні (за двома кутами).

У подібних  трикутників відповідні сторони пропорційні:

$\bf \dfrac{AB}{AM} =\dfrac{BC}{MN} =\dfrac{AC}{AN}$

Знайдемо коефіцієнт подібності.

• Коефіцієнт подібності (k) дорівнює співвідношенню відповідних сторін трикутників:

$\bf k=\dfrac{AB}{AM} =\dfrac{9}{6} =\dfrac{3}{2}$

Отже:

$\bf \dfrac{BC}{MN} =k\\\\\bf BC=MN\cdot k = 10\cdot \dfrac{3}{2} =5\cdot 3=15$

BC = 15 см

$\bf \dfrac{AC}{AN} =k\\\\\bf AC=AN\cdot k = 9\cdot \dfrac{3}{2} =\dfrac{27}{2}=13,5$

AC = 13,5 см

#SPJ1