Помогите пожалуйста, даю 10 баллов!!!!!
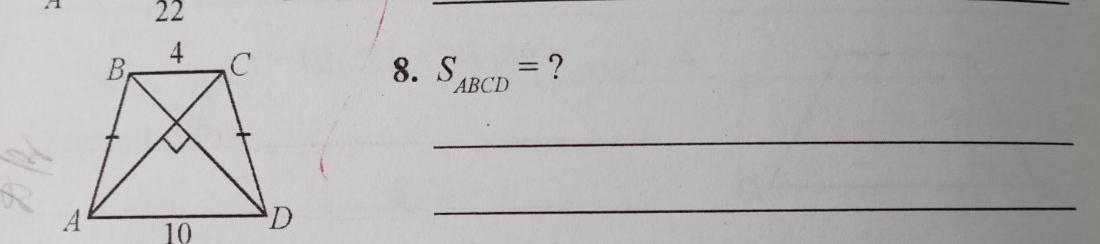
Ответы
Ответ:
Площадь трапеции равна 49 ед.²
Пошаговое объяснение:
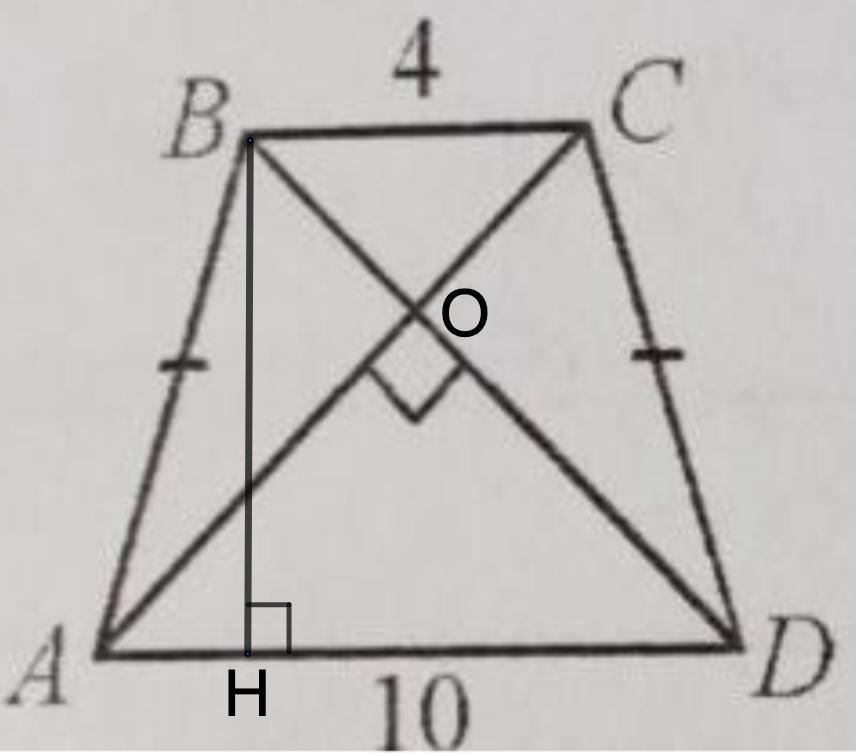
Решить задачу по чертежу.
Найти площадь ABCD.
Дано: АВСD - равнобедренная трапеция.
ВС = 4; AD = 10.
AC ⊥ BD.
Найти: S(ABCD)
Решение:
- Площадь трапеции равна произведению полусуммы оснований на высоту.
Основания известны, надо найти высоту.
Проведем высоту ВН.
1. Рассмотрим ΔABD и ΔACD.
AD - общая;
АВ = CD (АВСD - равнобедренная трапеция)
- В равнобедренной трапеции диагонали равны.
⇒ BD = AC.
ΔABD = ΔACD (по трем сторонам, 3 признак)
⇒ ∠CAD = ∠BDA (как соответственные элементы.
2. Рассмотрим ΔAOD - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠CAD = ∠BDA = 90° : 2 = 45°
3. Рассмотрим ΔНВD - прямоугольный.
∠HBD = 90° - 45° = 45°
- Если в треугольнике два угла равны, то этот треугольник равнобедренный.
⇒ ВН = HD.
- Высота, опущенная из вершины тупого угла к большему основанию, делит его на части, большая из которых равна полусумме оснований.
⇒ BH = HD = (BC + AD) : 2 = (4 + 10) : 2 = 7
Теперь можем найти площадь:
Площадь трапеции равна 49 ед.²
***
Можно решить проще, если воспользоваться свойством равнобедренной трапеции со взаимно перпендикулярными сторонами:
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований (высота равна средней линии).
⇒ (BC + AD) : 2 = BH = 7
А площадь равна:
S(ABCD) = 7 · 7 = 49 (ед.²)
#SPJ1