Предмет: Геометрия,
автор: kknzaaliza
ПОМОГИТЕ ПОЖАЛУЙСТА С ГЕОМЕТРИЕЙ!!!
Приложения:
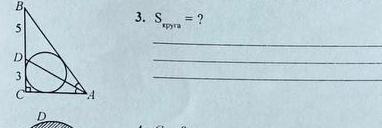
Ответы
Автор ответа:
0
Ответ:
Площадь круга равна 12,56 ед.²
Объяснение:
Найти S круга.
Дано: ΔСВА - прямоугольный.
AD - биссектриса;
CD = 3; DB = 5.
Окр. О,r - вписанная в ΔСВА.
Найти: S круга.
Решение:
Формула площади круга:
,
где r - радиус круга.
Радиус можем найти по формуле:
,
где a и b - катеты, с - гипотенуза.
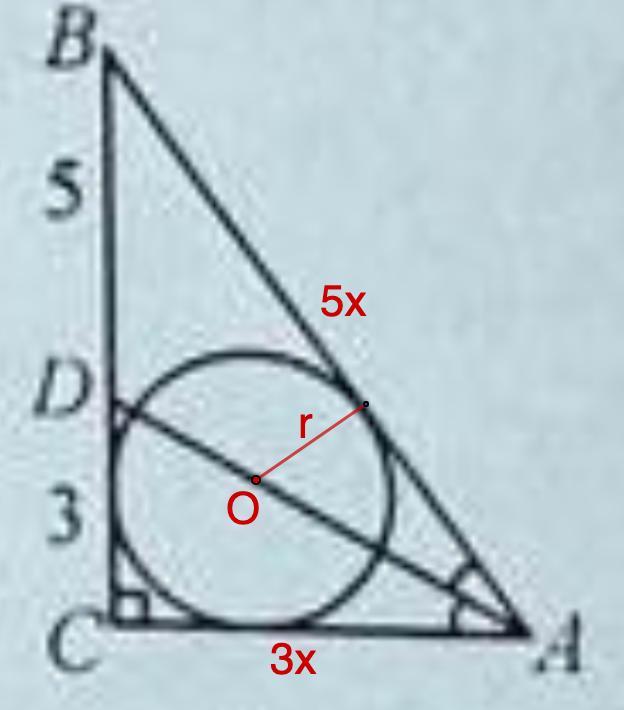
Итак, необходимо найти стороны треугольника СВА.
Рассмотрим ΔСВА - прямоугольный,
AD - биссектриса.
- Биссектриса делит противоположную сторону на части, которые пропорциональные прилегающим сторонам.
⇒
Пусть СА = 3х, тогда ВА = 5х.
По теореме Пифагора:
ВА² - СА² = СВ²
25х² - 9х² = (5+3)²
16х² = 64 |:16
x² = 4
x = 2
⇒ AB = 10; CA = 6
Найдем радиус вписанной окружности:
А теперь можем найти площадь круга:
Sк = π · 2² = 4π = 12,56 (ед.²)
Ответ: 12,56 ед.²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: alenadolgih659
Предмет: Английский язык,
автор: masdamssss
Предмет: Русский язык,
автор: аня2450
Предмет: Физика,
автор: viscas890
Предмет: Английский язык,
автор: saidsofiya567