Предмет: Алгебра,
автор: whatismyname28
ДАЮ 30 БАЛЛОВ!
Решите задачу:
Приложения:
Ответы
Автор ответа:
2
Ответ:
Меньший угол, который образовывается при пересечении этих биссектрис равен 80°.
Объяснение:
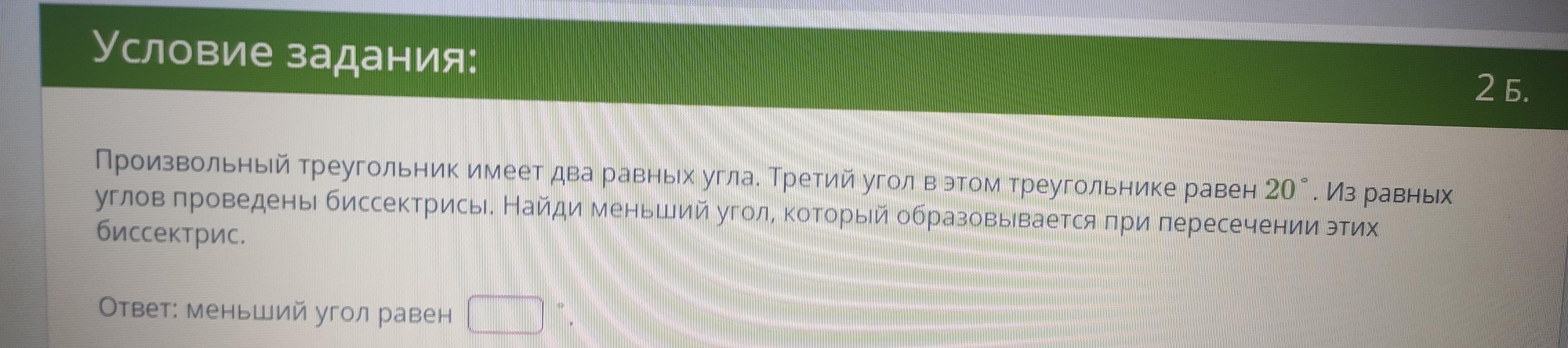
Произвольный треугольник имеет два равных угла. Третий угол в этом треугольнике равен 20. Из равных углов проведены биссектрисы. Найди меньший угол, который образовывается при пересечении этих биссектрис.
Дано: ΔАВС.
∠А = ∠С;
АН и СЕ - биссектрисы;
∠В = 20°
Найти: меньший угол, который образовывается при пересечении этих биссектрис.
Решение:
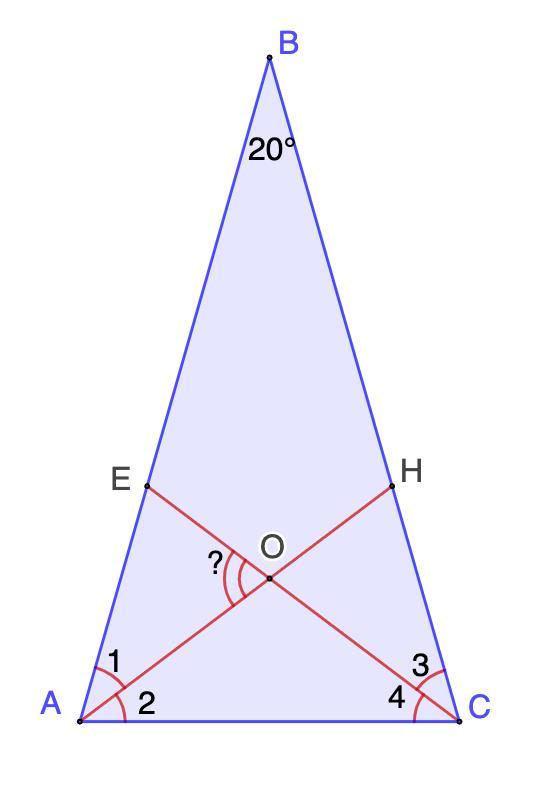
Обозначим ∠1, ∠2, ∠3, ∠4. (см. рис.)
∠А = ∠С (условие)
∠В = 20°
- Сумма углов треугольника равна 180°.
⇒ ∠А = ∠С = (180° - 20°) : 2 = 80°
Тогда
∠1 = ∠2 = ∠3 = ∠4 = 80° : 2 = 40°
∠АОЕ - внешний ΔАОС.
- Внешний угол равен сумме углов, не смежных с ним.
⇒ ∠АОЕ = ∠2 + ∠4 = 40° + 40° = 80°
∠АОЕ и ∠АОС - смежные.
- Сумма смежных углов равна 180°.
⇒ ∠АОС = 180° - 80° = 100°
Меньший угол, который образовывается при пересечении этих биссектрис равен 80°.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: murlyk
Предмет: Русский язык,
автор: sunrise4
Предмет: Окружающий мир,
автор: рома1072
Предмет: Геометрия,
автор: EinLegoMan
Предмет: Обществознание,
автор: sanlanmeneger