Предмет: Математика,
автор: oleksandrmaksimenko8
3.22. Знайдіть значення виразу (sin alpha - sin beta)/(cos alpha + cos beta) якщо alpha - beta = pi/2
Приложения:
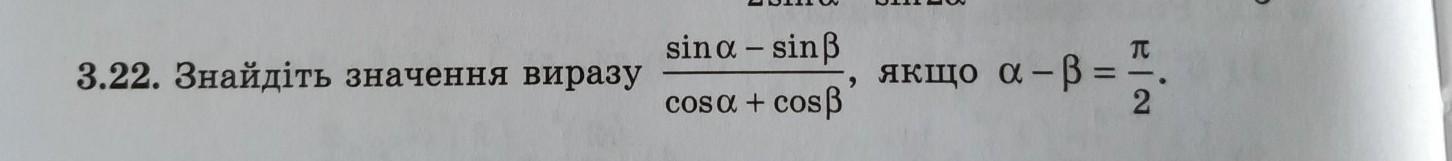
Ответы
Автор ответа:
0
Формулы приведения:
Рассмотрим заданное соотношение:
Выразим из этого соотношения одну из переменных, например, :
Подставим в искомое выражение и, применяя формулы приведения, получим:
Ответ: 1
Похожие вопросы
Предмет: Русский язык,
автор: MkmariA
Предмет: Русский язык,
автор: ManglLove
Предмет: Английский язык,
автор: love0108
Предмет: Математика,
автор: firuzamadalieva2006
Предмет: Русский язык,
автор: Hrystim