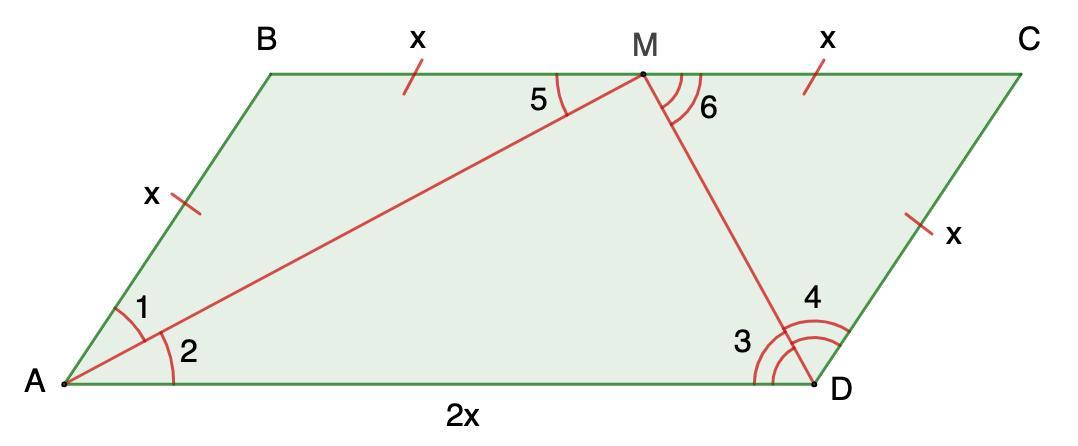
Бісектриси кутів А та D парелелограма ABCD перетинаються в точці М, яка лежить на стороні ВС. Знайти сторони парелелограма, якщо його периметр дорівнює 36 см.
Ответы
Ответ:
Стороны параллелограмма равны: АВ = CD = 6 см; ВС = AD = 12 см.
Объяснение:
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке М, которая лежит на стороне ВС. Найти стороны параллелограмма, если его периметр равен 36 см.
Дано: ABCD - параллелограмм;
АМ и DM - биссектрисы уголов А и D соответственно;
АМ ∩ DM = М; М ∈ ВС;
Р (ABCD) = 36 см.
Найти: стороны АВСD.
Решение:
Обозначит углы 1, 2, 3, 4, 5, 6. См. рис.
1. Рассмотрим ΔАВМ.
∠2 = ∠1 (АМ - биссектриса)
∠2 = ∠5 (накрест лежащие при BC || AD и секущей АМ)
⇒ ∠1 = ∠5
- Если в треугольнике два угла равны, то этот треугольник равнобедренный.
⇒ АВ = ВМ.
2. Рассмотрим ΔMCD.
∠3 = ∠4 ( DМ - биссектриса)
∠3 = ∠6 (накрест лежащие при BC || AD и секущей DМ)
⇒ ∠4 = ∠6
ΔMCD - равнобедренный.
⇒ МС = CD.
3. Рассмотрим ABCD - параллелограмм.
Пусть АВ = х см.
АВ = ВМ = х см. (п.1)
- Противоположные стороны параллелограмма равны.
⇒ АВ = CD = x см.
CD = МС = х см (п.2)
Тогда стороны ABCD равны:
АВ = CD = x см
ВС = AD = 2x см
- Периметр - сумма длин всех сторон параллелограмма.
Р(ABCD) = АВ + CD + ВС + AD = 6x = 36 см
6х = 36
х = 6
АВ = CD = 6 см
ВС = AD = 12 см
Стороны параллелограмма равны: АВ = CD = 6 см; ВС = AD = 12 см.
#SPJ1