Question

Решите люди добрые !!! Дам 20 балов

Answer 1

Ответ:

(-∞; 3]

Пошаговое объяснение:

Решить неравенство

$\left| \dfrac{x-2}{x-4}\right |\leq 1$

$-1\leq \dfrac{x-2}{x-4}\leq 1$

Так как знаменатель дроби отличен от нуля, то

$x-4\neq 0;\\x\neq 4.$

Значит, ОДЗ : (-∞; 4) ∪(4; + ∞)

Данное неравенство равносильно системе:

$\left \{\begin{array}{l} \dfrac{x-2}{x-4} \geq -1 ,\\\\ \dfrac{x-2}{x-4} \leq 1\end{array} \right.$

Решим каждое неравенство системы отдельно

$1) \dfrac{x-2}{x-4}\geq -1;\\\\ \dfrac{x-2}{x-4}+1\geq 0;\\\\ \dfrac{x-2+x-4}{x-4}\geq 0;\\\\ \dfrac{2x-6}{x-4}\geq 0;\\\\ \left [\begin{array}{l} x \leq 3 , \\ x > 4 \end{array} \right.$

$2) \dfrac{x-2}{x-4}\leq 1;\\\\ \dfrac{x-2}{x-4}-1\leq 0;\\\\ \dfrac{x-2-x+4}{x-4}\leq 0;\\\\ \dfrac{2}{x-4}\leq 0;\\\\ x-4 < 0 ;\\x < 4.$

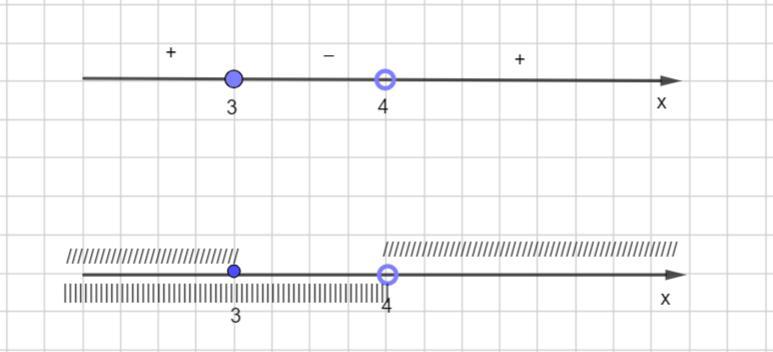
Найдем общее решение ( во вложении)

$x\leq 3$

x ∈(-∞; 3]