Question

Памагити!!
задана функция y=x²— 6x+7
выберете верные утверждения которые относятся к этой функции:

1 Точка пересечения графика функции с осью Oy: (0,7)

2 E(y):(2,∞)

3 область определения функции- вся действительная ось

4 E(y):[—2,∞)

5 график функции не пересекает ось абсцисс

6 график функции пересекает ось абсцисс в двух точках ​

Answer 1

Ответ:

верны утверждения 1);  3);  4); 6)

Объяснение:

y = x² -  6x + 7

1) Точка пересечения графика функции с осью OY: (0,7)

Точка пересечения графика функции с осью ОY - это точка с координатами (0; y).

Т.е. это точки значения функции при х = 0.

Подставим х = 0 в наше уравнение.

y = 0² -  6*0 + 7 = 7

Таким образом, точка пересечения графика функции с осью OY - точка (0; 7)

Утверждение  верно.

2) E(y): (2,∞)

Наша функция - это парабола ветвями вверх.

Ее вершина считается по формуле  у₀ = х₀² +bx₀ + c, где  $\displaystyle x_0=\frac{-b}{2a} ;$.

В нашем случае  

$\displaystyle x_0=\frac{-(-6)}{2} =3;\qquad y_0=3^2-6*3+7=9-18+7=-2$

Таким образом, вершина параболы находится в точке (3; -2), и, следовательно, область значений данной функции  

E(y):  {y ∈ R: у ≥ -2}  или  E(y): [—2,∞)

Утверждение не верно.

3) область определения функции- вся действительная ось.

В данном случае ограничений на аргумент х не налагается, поэтому область определения функции - это вся действительная ось.

Утверждение верно.

4 ) E(y):  [—2,∞)

Мы уже определили выше область значения функции.

Поэтому, утверждение верно

5) график функции не пересекает ось абсцисс.

График функции пересекает ось абсцисс в точках с координатами  (хₙ; 0)

Т.е. это точки, где функция равна 0.

Другими словами это хₙ - это корни уравнения x² -  6x + 7 = 0.

Сколько корней  у нашего уравнения?

Посмотрим на дискриминант уравнения.

$\displaystyle x^2 - 6x + 7 = 0\\D = b^2-4ac ;\quad D=(-6)^2-4*7=36-28=8$

D ≠0, D > 0, следовательно, уравнение имеет два корня, и график функции пересекает ось абсцисс в двух точках.

Другое объяснение.

График функции - это парабола ветвями вверх. ее вершина лежит ниже оси абсцисс, в точке (3; -2) (пункт 2). Таким образом, график функции пересечет ось абсцисс в двух точках.

Утверждение не верно

6) график функции пересекает ось абсцисс в двух точках .

См п. 5)

Утверждение  верно .

Вывод: верны утверждения 1);  3);  4); 6)

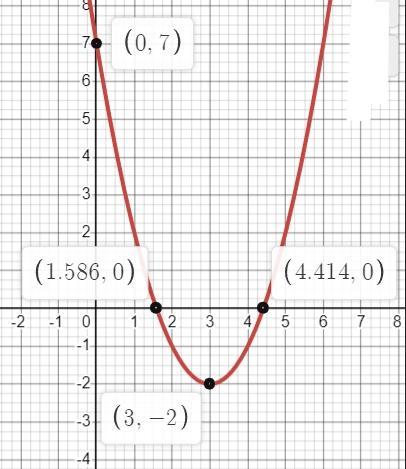
График функции на всякий случай прилагается.

SPJ1