Question

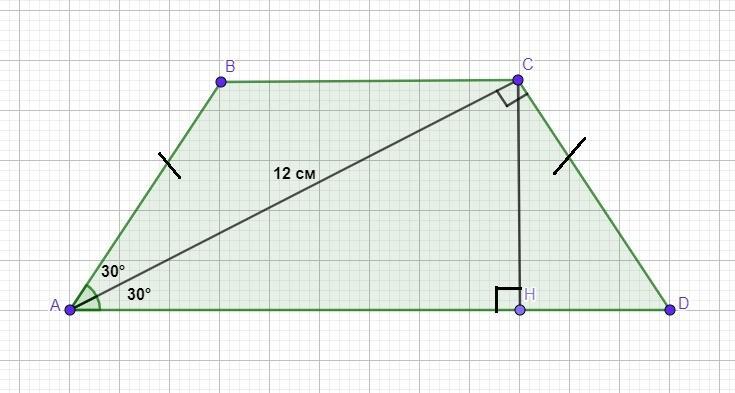
Діагональ рівнобічної трапеції дорівнює 12 см. перпендикулярна до бічної сторони і є бісектрисою кута при основі, який дорівнює 60º. Знайдіть площу трапеції.

Answer 1

Ответ:

Площа трапеції дорівнює 36√3 см²

Объяснение:

Діагональ рівнобічної трапеції дорівнює 12 см, перпендикулярна до бічної сторони і є бісектрисою кута при основі, який дорівнює 60º. Знайдіть площу трапеції.

Дано: ABCD - трапеція, ВС║AD, АВ=CD. Діагональ АС=12 см. АС - бісектриса ∠А. ∠А=60° ⇒ ∠АВС=∠САD=30° - за означенням бісектриси.

АС⊥CD.

Знайти: S(ABCD).

Проведемо CH⊥AD. CH - висота  ABCD, тоді

• Площа трапеції обчислюється за формулою:

$\boxed{S=\dfrac{BC+AD}{2} \cdot CH}$

1) Розглянемо прямокутний трикутник ACD(∠C=90°).

• Тангенсом гострого кута α прямокутного трикутника називають відношення катета, прилеглого до кута α, до катета, протилежного куту α.

$tg \angle CAD=\dfrac{CD}{AC} \\\\CD=AC\cdot tg \angle CAD=12\cdot tg 30^\circ = 12\cdot\dfrac{\sqrt{3} }{3 } =4\sqrt{3}$

CD = 4√3 cм

CD - катет, протилежний куту ∠САD=30°.

• Якщо у прямокутному трикутнику один з гострих кутів дорівнює 30°, то протилежний цьому куту катет буде дорівнювати половині гіпотенузи.

Тому гіпотенуза AD = 2·CD = 2·4√3 = 8√3 см

2) Розглянемо прямокутний трикутник ACН(∠Н=90°).

CН - катет, протилежний куту ∠САН=30°, гіпотенуза АС = 12 см, тому:

$CH=\dfrac{1}{2} AC=\dfrac{12}{2} =\bf 6$    см

3) За означенням бісектриси ∠BAC=∠CAD, BC||AD, AC- січна, тому ∠BCA=∠CAD - як різносторонні кути.

Оскільки гострі кути в трикутнику ABC рівні, то він рівнобедрений. Звідси AB=BC=CD=4√3 см

4) Знаходимо площу трапеції:

$S=\dfrac{4\sqrt{3} +8\sqrt{3} }{2} \cdot 6=\dfrac{12\sqrt{3} }{2} \cdot 6=\bf 36\sqrt{3}$    cм²

Площа ABCD дорівнює 36√3 см²

#SPJ1