СРОЧНОО
1) у рівнобедреному трикутнику MKE (MK = KE) бісектриса кута E
перетинає сторону MK у точці C. Знайдіть кути трикутника MKE,
якщо
2) Периметр
трикутника ABC, описаного навколо кола, дорівнює 30 см. Точка дотику
кола зі стороною AB ділить її у відношенні 3 : 2, рахуючи від точки A,
а точка дотику зі стороною BC віддалена від точки C на 5 см.
Знайдіть сторони трикутника.
Ответы
Ответ:
1) Углы треугольника МКЕ равны 84°, 84°, 12°.
2) Стороны треугольника равны 10 см, 9 см, 11 см.
Объяснение:
Уточненное задание.
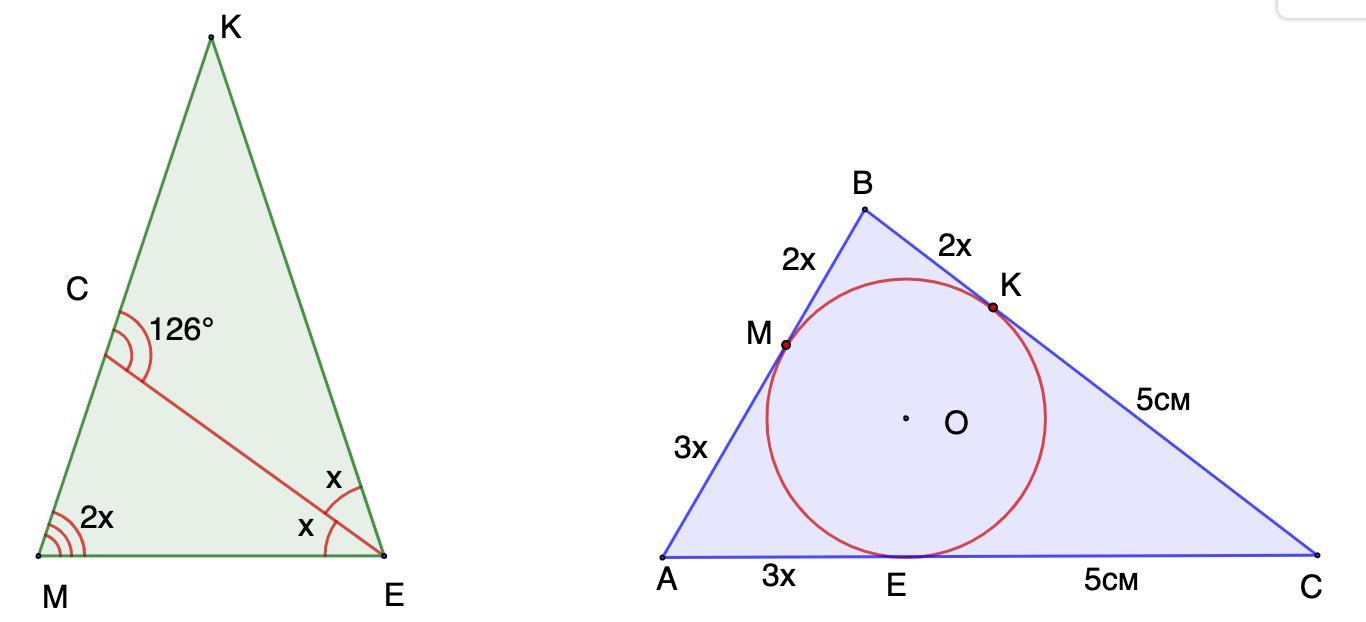
1) В равнобедренном треугольнике МКЕ (MK = KE) биссектриса угла E пересекает сторону MK в точке C. Найдите углы треугольника MKE, если ∠KCE = 126°.
2) Периметр треугольник ABC, описанного около окружности, равен 30 см. Точка касания окружности со стороной AB делит ее в отношении 3 : 2, считая от точки A, а точка касания со стороной BC удалена от точки C на 5 см. Найдите стороны треугольника.
1) Дано: ΔМКЕ - равнобедренный;
MK = KE;
ЕС - биссектриса;
∠KCE = 126°.
Найти: углы ΔМКЕ.
Решение:
Пусть ∠МЕС = ∠СЕК = х (ЕС - биссектриса)
⇒ ∠Е = 2х
- В равнобедренном треугольнике углы при основании равны.
⇒ ∠М = ∠Е = 2х
Рассмотрим ΔМСЕ.
∠KCE = 126° - внешний угол ΔМСЕ.
- Внешний угол треугольника равен сумме углов, не смежных с ним.
⇒ ∠KCE = ∠М + ∠МЕС = х + 2х = 126°
3х = 126°
х = 42°
⇒ ∠М = ∠Е = 2х = 84°
- Сумма углов треугольника равна 180°.
⇒ ∠К = 180° - (84° + 84°) = 12°
Углы треугольника МКЕ равны 84°, 84°, 12°.
2) Дано: ΔАВС.
Окр.О - вписана в ΔАВС;
М и К - точки касания.
АМ : МВ = 3 : 2
КС = 5 см.
Р(АВС) = 30 см.
Найти: стороны ΔАВС.
Решение:
Рассмотрим ΔАВС.
АМ : МВ = 3 : 2
Пусть АМ = 3х см, тогда МВ = 2х см.
- Отрезки касательных, проведенных из одной точки, равны.
⇒ АМ = АЕ = 3х см, МВ = ВК = 2х, КС = ЕС = 5 см.
- Периметр треугольника - сумма длин его сторон.
⇒ Р(АВС) = АВ + ВС + АС = АМ + МВ +ВК + КС + АЕ + ЕС =
= 3х + 2х + 2х + 5 + 3х + 5 = 10х + 10 (см)
Р(АВС) = 30 см
10х + 10 = 30
10х = 20
х = 2
АВ = 3х + 2х = 5х = 10 (см)
ВС = 2х + 5 = 9 (см)
АС = 3х + 5 = 11 (см)
Стороны треугольника равны 10 см, 9 см, 11 см.
#SPJ1