Предмет: Математика,
автор: msheka00
Срочно помогите упростить выражение!!ДАЮ 48 БАЛЛОВ
Приложения:
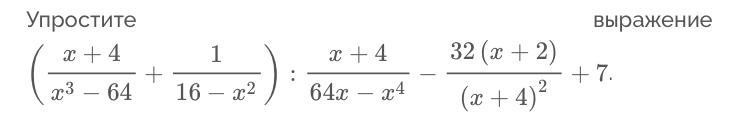
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Упростить:
Для решения вспомним формулы сокращенного умножения:
a³ - b³ = (a - b)(a² + ab + b²)
a² - b² = (a - b)(a + b)
(a + b)² = a² + 2ab + b²
Сначала упростим выражении в скобке:
Выполним деление. Вынесем в знаменателе делителя х за скобку:
А теперь все остальное:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: annadavletchtn
Предмет: Русский язык,
автор: Бонька205
Предмет: Окружающий мир,
автор: Аноним
Предмет: Английский язык,
автор: Аноним