Предмет: Алгебра,
автор: sia742
При каких значениях х производная функции больше нуля?
Приложения:
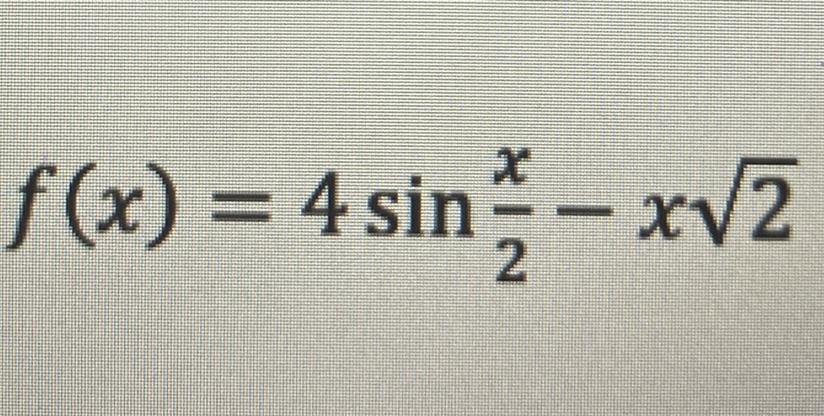
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: 65765
Предмет: Українська мова,
автор: егорашик
Предмет: Русский язык,
автор: Hayam
Предмет: Математика,
автор: nikolmolotkova2017
Предмет: Физика,
автор: minerjaml5