Предмет: Алгебра,
автор: crazydogwowwow
Огромная просьба пожалуйста как можно понятнее и развернуто дайте ответ
Приложения:
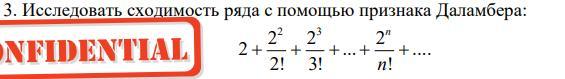
Ответы
Автор ответа:
1
Ответ:
ряд сходится.
Объяснение:
В соответствии с признаком Даламбера, найдём значение выражения :
Поскольку по признаку Даламбера ряд сходится.
Похожие вопросы
Предмет: Русский язык,
автор: МилАнна1
Предмет: Русский язык,
автор: айша61
Предмет: Английский язык,
автор: yaantonio19
Предмет: Математика,
автор: xboksnikita
Предмет: Математика,
автор: arinavv505