Question

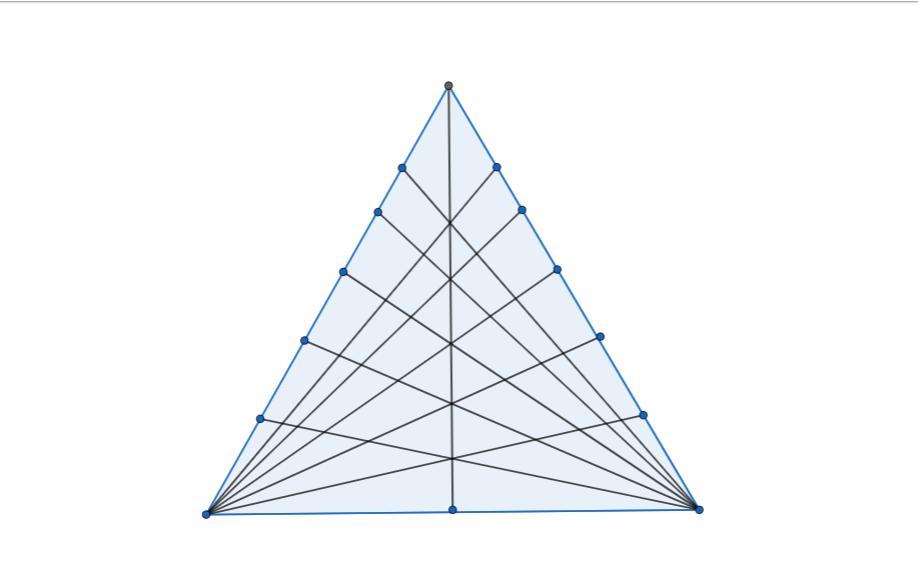
Посчитайте кол-во треугольников на первом рисунке , и также выведите общую формулу решения для данной задачи в зависимости от количества отрезков, проведенных из n-го кол-ва отрезков на сторонах большего треугольника . ( к примеру как на втором рисунке , чтобы с помощью данной формулы можно было бы посчитать кол-во треугольников )

Answer 1

Ответ:

175;      $n^3+2n^2.$

Пошаговое объяснение:

Сразу перейдем к выводу общей формулы для числа таких треугольников. Зададимся вопросом - когда три прямые на плоскости определяют треугольник. Для этого существует только два ограничения - когда среди прямых есть параллельные, и когда эти прямые проходят через одну точку.

Конечно, в нашем случае мы имеем не прямые, а отрезки, но если их продолжить до бесконечности, новых точек пересечения не будет и поэтому новые треугольники не возникнут. Почему мы в этом уверены? Да просто две различные прямые не могут иметь две общие точки, а по одной общей точке эти прямые имеют уже в пределах чертежа.   Кстати, на нашей картине параллельных прямых нет, так что об этом можно не думать.

Разберемся сначала, сколько всего прямых мы имеем. Пусть боковые стороны разбиты точками пересечения на n частей (иными словами, на каждой боковой стороне мы имеем k=n+1 точек пересечения прямых). Конечно, высота будет разбита также на  n отрезков (то, что это высота, абсолютно не принципиально, как и то, равнобедренный это треугольник или нет). Кроме четырех прямых, идущих по сторонам треугольника и по его "высоте", мы имеем (n-1) прямую, проходящую через левую вершину, и (n-1) прямую, прохордящую через правую вершину. Всего получается 2n+2=2k прямых. Сколько мы имеем троек прямых? На этот вопрос давно получен ответ в науке под названием комбинаторика - их ровно

             $C_{2k}^3=\dfrac{(2k)!}{3!\cdot (2k-3)!}=\dfrac{2k\cdot (2k-1)\cdot (2k-2)}{6}$.

Из этого количества нужно удалить тройки прямых, проходящих  через одну точку.  Среди таких троек $C_k^3$ троек, проходящих через левую вершину, $C_k^3$. троек, проходящих через правую вершину, и

(k-1) тройка, проходящая через ту или иную точку "высоты".

В результате получаем ответ на вопрос о количестве треугольников - их

  $C_{2k}^3-2C_k^3-(k-1)=C_{2(n+1)}^3-2C_{n+1}^3-n$.

В частности, если n=1 (то есть k=2) - это когда просто нарисован треугольник с "высотой", мы имеем 3 треугольника. Конечно, формально в этом случае формула не работает, но если считать, что число сочетаний из 2 по 3 равно 0, формула даст правильный ответ.

При n=2 (k=3) получаем

  $C_{6}^3-2C_3^3-2=\dfrac{6\cdot 5\cdot 4}{6}-2-2=16,$

что легко проверяется непосредственным подсчетом.

При n=3 (k=4) формула дает 45 треугольника.

При n=4 (k=5) получается  96 треугольников.  

При n=5 (k=6) получается 175 треугольников.    

Кстати, если раскрыть числа сочетаний, ответ можно записать и в таком виде:

                                              $n^3+2n^2.$