Question

Площадь боковой поверхности правильной треугольной призмы равна 324 см, площадь полной поверхности этой же призмы равна - 36(9+√3) см.
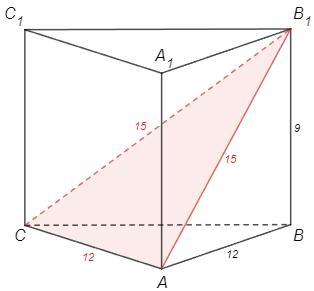
Найдите площадь сечения, проведённого через сторону нижнего основания и противоположную вершину верхнего основания.

Answer 1

Правильная треугольная призма: в основании правильный треугольник, боковые грани - равные прямоугольники.

Sполн =Sбок +2*Sосн =36(9+2√3) =324 +36*2√3 => Sосн =36√3

S(ABC) =AB^2 √3/4 =36√3 => AB =√(36*4) =12 =AC

S(АА1B1B) =Sбок/3 =324/3 =108

BB1 =S(АА1B1B)/AB =108/12 =9

AB1 =√(AB^2+BB1^2) =15 =CB1

S(AB1C), ф Герона

p =(a+b+c)/2 =(12+15+15)/2 =21

S =√(p(p-a)(p-b)(p-c)) =√(21*9*6*6) =18√21