Question

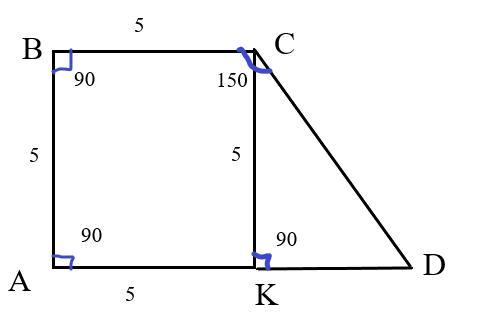
1. В трапеции ABCD известно, что ∠В = 90°, ∠C= 150°, ВС =5 см. Найдите сторону CD, если высота трапеции, проведённая из вершины С, разбивает данную трапецию на треугольник и квадрат
2

Answer 1

Ответ:

CD=10 см

Пошаговое объяснение:

Дано: ABCD - трапеция, ∠АВС=90°, ∠BCD=150°, ВС=5 см, СК- высота

Найти:  CD-?

Решение:

Так как АВСD- квадрат (по условию), то

АВ=ВС=СК=АК=5 см,

∠АВС=∠ВАК=∠АКС=∠ВСК=90°

∠KCD=∠BCD-∠BCK=150°-90°=60°

Рассмотрим ΔKCD

Так как СК- высота, то ΔKCD - прямоугольный (∠СКD=90°)

∠KCD = 60°

∠CDK=180°- ∠СКD-∠KCD = 180°-90°-60° =30°

CK=$\frac{1}{2}$ CD (как катет, что лежит против угла в 30°)⇒

CD=2СК = 2*5=10 см

Ответ: CD=10 см