Question

Расстояния от точек А и В до плоскости соответственно равны 12,5 см и 3,5 см. Длина проекции отрезка АВ на эту плоскость рана 12 см Найдите расстояние между точками А и В. Рассмотрите в обоих случаях

Answer 1

Объяснение:

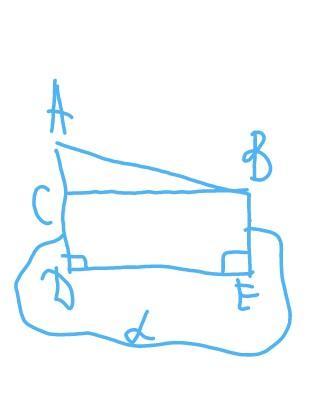
1) когда не пересекает плоскость:

АD=12,5 см

ВЕ=3,5 см

СВ=12 см

найти: АВ

АС=АD-BE=12,5-3,5=9 см

по теореме Пифагора:

АВ=√(АС²+СВ²)=√(9²+12²)=√225=15см

ответ: АВ=15 см

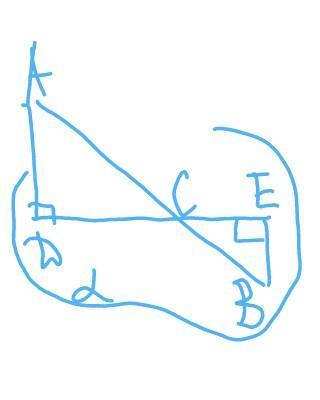
2)

когда пересекает плоскость:

DE=12 см

АD=12,5 cм

ВЕ=3,5 см

∆АDC~∆BEC по углам

k=BE/AD=3,5:12,5=0,28 см

пусть СЕ=х см,тогда DC=DE-CE=(12-x) см

СЕ/DC=k

x/(12-x)=0,28

x=0,28(12-x)

x=3,36-0,28x

x+0,28x=3,36

1,28x=3,36

x=2,625 cм СЕ

DC=12-2,625=9,375 см

рассмотрим ∆АDC- прямоугольный:

по теореме Пифагора:

АС=√(АD²+DC²)=√(12,5²+9,375²)=

=√(156,25+87,890625)=√244,140625=

=15,625 cм

∆ ВЕС -прямоугольный

по теореме Пифагора:

ВС=√(СЕ²+ВЕ²)=√(2,625²+3,5²)=

=√19,140625=4,375 см

АВ=АС+ВС=15,625+4,375=20 см

ответ: АВ=20 см