Question

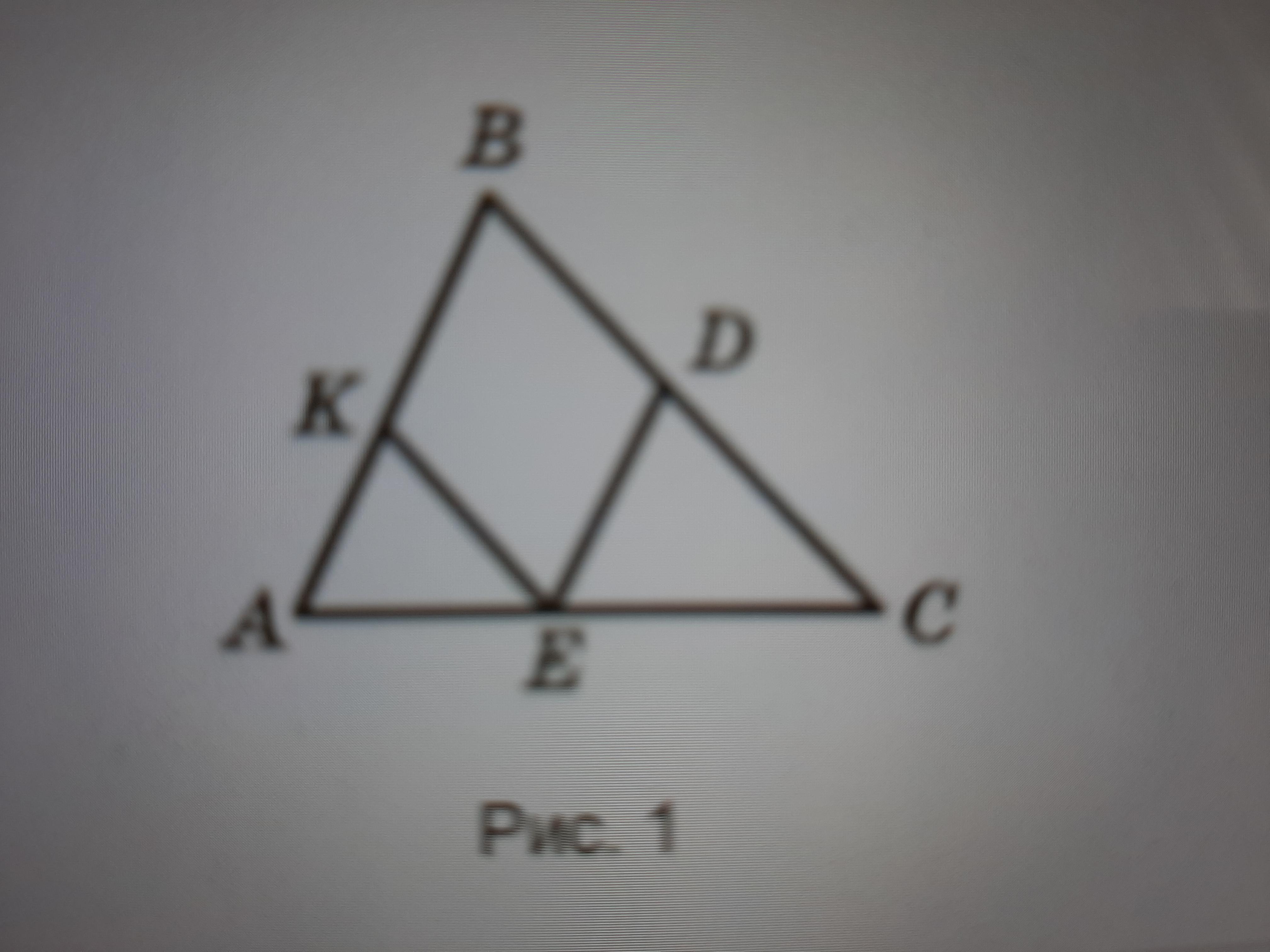
На рисунку зображено трикутник ABC і вписаний у нього ромб BDEK. Знайдіть сторону ромба, якщо AB = 10 см, BC = 15 см

Answer 1

Ответ:

Сторона ромба равна 6 см

Объяснение:

Пусть сторона ромба равна $x$, тогда $AK = AB - KB = 10 - x$, $DC = BC - BD = 15 - x$.

Так как $AB\parallel DE$ и $BC\parallel KE$, то треугольники $AKE$ и $EDC$ подобны,

$\displaystyle\frac{{AK}}{{KE}} = \displaystyle\frac{{ED}}{{DC}};\\\\\displaystyle\frac{{10 - x}}{x} = \displaystyle\frac{x}{{15 - x}};\\\\(10 - x)(15 - x) = {x^2};\\\\150 - 15x - 10x + {x^2} = {x^2};\\\\25x = 150;\\\\x = 6.$

Answer 2

Відповідь: 6 см.

Пояснення: розв'язання завдання додаю