Question

перечислить все значения a, при которых уравнение будет иметь корень sin⁴x+cos⁴x=asinxcosx.​

Answer 1

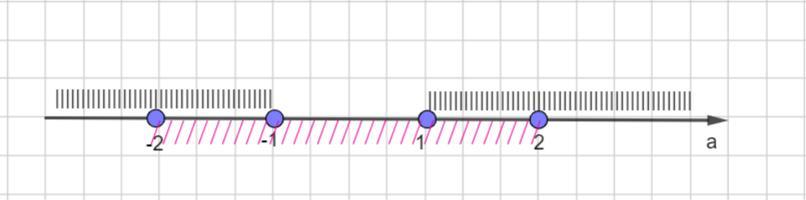
Ответ:

a ∈ [-2; -1] ∪ [1; 2 ]

Пошаговое объяснение:

Найти при каких значениях а уравнение будет иметь корни

$sin^{4} x+cos^{4} x =asinx\cdot cosx$

Преобразуем левую часть уравнения, для этого воспользуемся основным тригонометрическим тождеством $sin^{2} x+cos ^{2} x=1$

и формулой сокращенного умножения $(a+b) ^{2} =a^{2} +2ab+b^{2}$

$sin^{4} x+cos^{4} x =asinx\cdot cosx;\\(sin^{2} x)^{2} +(cos^{2} x )^{2}+2sin ^{2} x\cdot cos^{2} x-2sin ^{2} x\cdot cos^{2} x =asinx\cdot cosx;\\(sin^{2} x+cos ^{2} x)^{2} -2sin ^{2} x\cdot cos^{2} x =asinx\cdot cosx;\\1 -2sin ^{2} x\cdot cos^{2} x =asinx\cdot cosx$

Воспользуемся формулой синуса двойного угла

$sin2x =2\cdot sinx\cdot cosx$

$sin^{2} 2x =4\cdot sin^{2} x\cdot cos^{2} x$

$1 -2sin ^{2} x\cdot cos^{2} x =asinx\cdot cosx|\cdot 2 ;\\2 -4sin ^{2} x\cdot cos^{2} x =2asinx\cdot cosx;\\2-sin^{2} 2x=asin2x;\\sin^{2} 2x+asin2x-2=0$

Получили квадратное уравнение относительно синуса 2х. Чтобы квадратное уравнение имело корни, дискриминант должен быть неотрицательным .

Так как $|sin2x|\leq 1$, то эти корни должны быть заключены в отрезке от -1 до 1.

Пусть $sin2x=t, |t|\leq 1$ , тогда уравнение принимает вид:

$t^{2} +at-2 =0$

$D= a^{2} -4\cdot1\cdot(-2) =a^{2} +8 > 0$

при любых значениях а , так как квадрат числа есть число неотрицательное

Проверим условие , что корни этого уравнения  заключены в отрезке от -1 до 1.

Рассмотрим функцию  $f(t) =t^{2} +at-2$

$\left \{\begin{array}{l} f(1) \geq 0, \\f(-1) \geq 0; \end{array} \right.\Leftrightarrow \left \{\begin{array}{l} 1+a-2 \geq 0, \\1-a-2 \geq 0; \end{array} \right.\Leftrightarrow \left \{\begin{array}{l} a-1 \geq 0, \\-a-1 \geq 0; \end{array} \right.\Leftrightarrow \left \{\begin{array}{l} a\geq 1, \\a\leq - 1; \end{array} \right.\Leftrightarrow$

Вершина параболы тоже должна быть заключена в отрезке от -1 до 1.

$t{_0}= \dfrac{-b}{2a} ;\\\\t{_0}= \dfrac{-a}{2}$

Тогда

$-1\leq -\dfrac{a}{2} \leq 1|\cdot (-2) \\-2\leq a\leq 2$

Тогда найдем решение системы

$\left \{\begin{array}{l} a \geq 1, \\ a \leq -1\\ -2\leq a\leq 2 ;\end{array} \right.\Leftrightarrow\left [\begin{array}{l} -2\leq a\leq -1, \\ 1\leq a\leq 2\end{array} \right.$