Question

Помогите решить задачу, заранее спасибо!
Высота равнобедренного треугольника проведенная к боковой стороне равна 5,2 см, а боковая сторона 10,4 см. Найдите углы треугольника

Answer 1

Ответ:

Формулы площади треугольника:

S=(a*h)/2

S=(a*b*sin(θ))/2

S=(5,2*10,4)/2=27,04

Найдем, по второй формуле площади, угол между двумя боковыми сторонами.

(10,4*10,4*sin(α))/2=27,04

54,08*sin(α)=27,04

sin(α)=1/2

α=arcsin(1/2)

α=30°

Углы при основании равны и сумма внутренних углов треугольника 180°.

30°+β+β=180°

2β=150°

β=75°

Углы треугольника: 30°; 75°; 75°

Answer 2

Ответ:

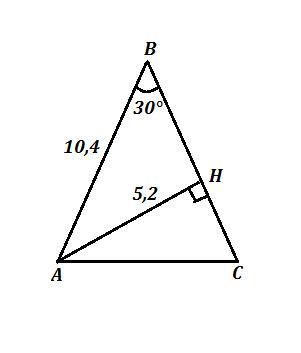
ΔАВС ,  АВ=ВС=10,4 см  ,   АН⊥ ВС ,   АН=5,2 см .

Найти углы ΔАВС .

     Так как  АН ⊥ ВС , то  ∠АНВ=90°  и ΔАНВ - прямоугольный , в котором катет АН=5,2 см , а гипотенуза АВ=10,4 см .

Заметим, что  10,4=2*5,2 , то есть катет АН равен половине гипотенузы . Значит угол, лежащий против такого катета равен 30°

∠АВН=∠В=30° .

Углы при основании равнобедренного треугольника равны.

Значит,  ∠А=∠С==(180°-30°):2=150°:2=75°

Ответ:  о∠А=75° , B=30° , ∠C=75° .