Предмет: Алгебра,
автор: QwertyLokom2
Решите с помощью формулы сокращенного умножения
Приложения:
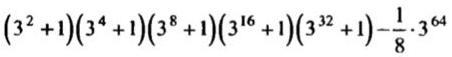
Ответы
Автор ответа:
1
Ответ:
решение смотри на фотографии
Приложения:

Автор ответа:
0
Решение .
Домножим и разделим уменьшаемое на , чтобы воспользоваться формулой разности квадратов
.
Похожие вопросы
Предмет: Другие предметы,
автор: liliyakhakimova
Предмет: Английский язык,
автор: Aline1906777
Предмет: Қазақ тiлi,
автор: gulnaztlegenova04
Предмет: Русский язык,
автор: dyachkov2007