Предмет: Геометрия,
автор: elarej01
помогите решить пожалуйста!!
Приложения:
ReMiDa:
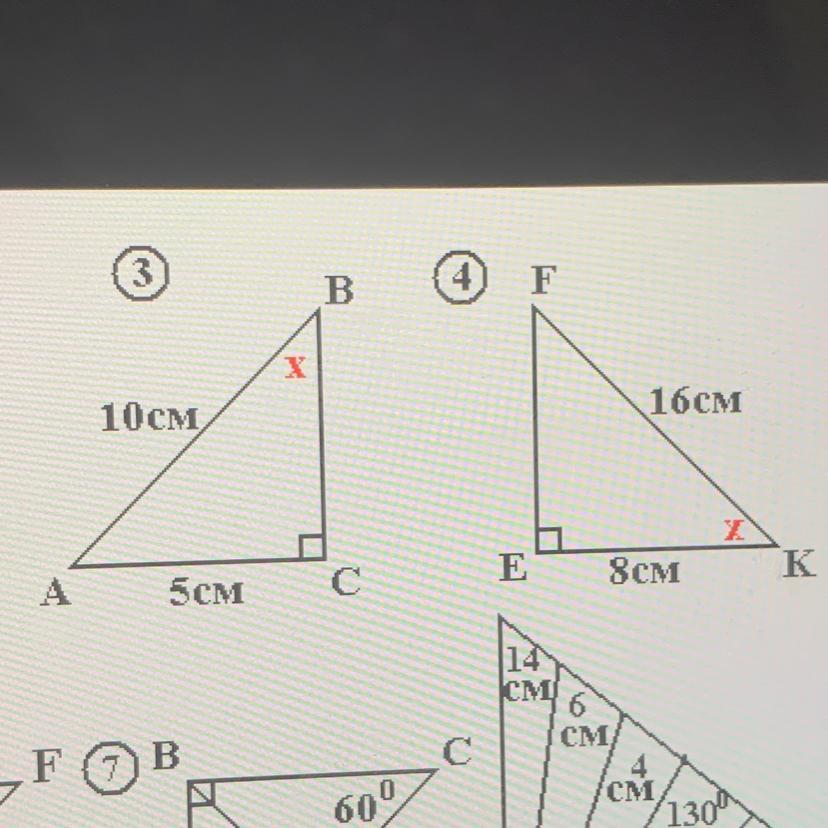
3) АС=½•АВ. Катет, равный половине гипотенузы лежит напротив угла 30°. Угол В=30°.
4) Угол F=30°, Следовательно Угол К=90°-30°=60° - так как сумма острых углов в прямоугольном треугольнике равна 90°
Ответы
Автор ответа:
1
Ответ:
3) 30°
4)60°
Объяснение:
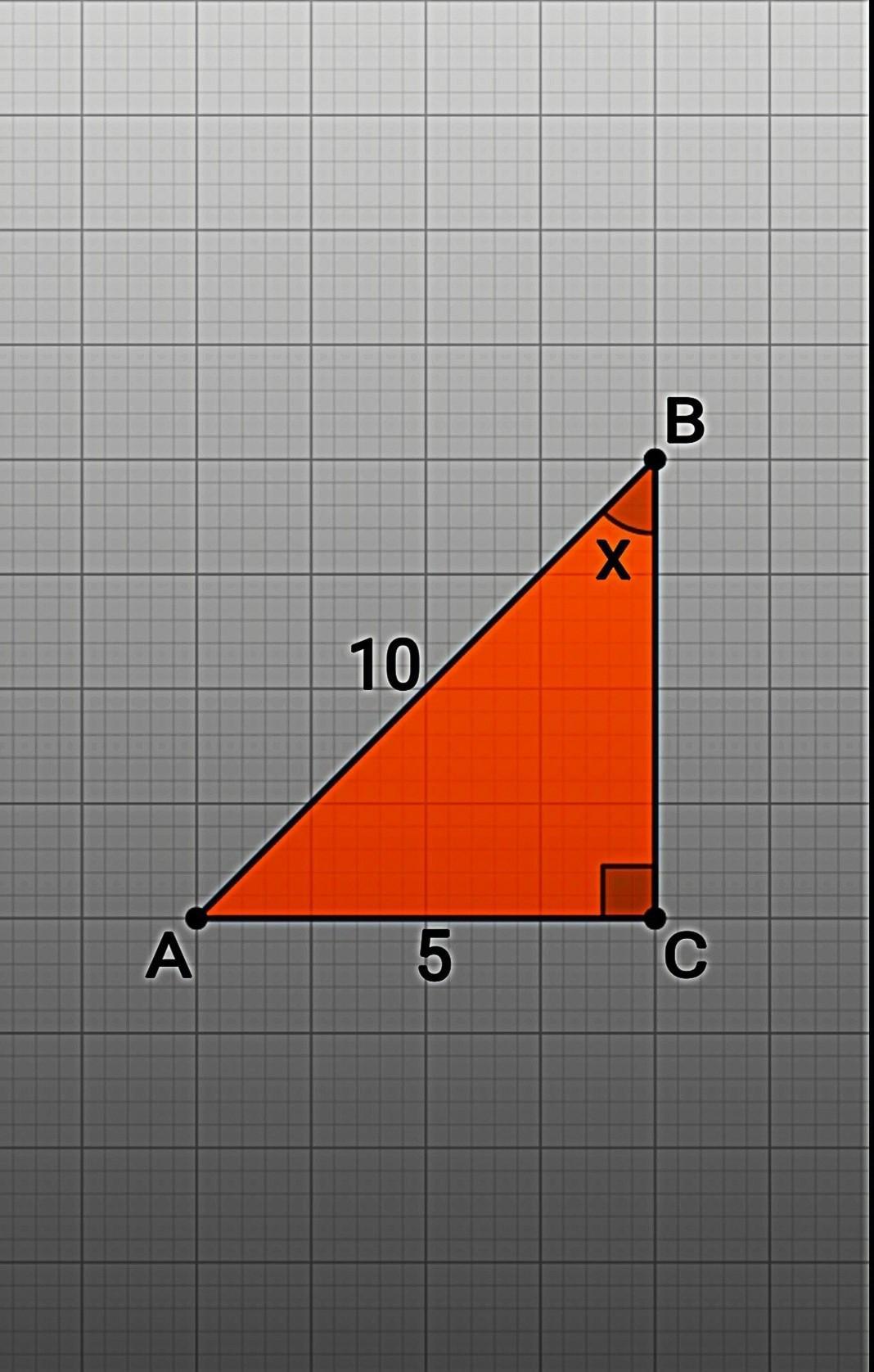
3)⠀Дано: АВ = 10см, АС = 5см, ∠С = 90°
⠀⠀Найти: ∠Х – ?
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение
- Катет лежащий против угла в 30° равен половине гипотенузы. АВ = 2АС. Следовательно ∠х = 30°
Второй способ:
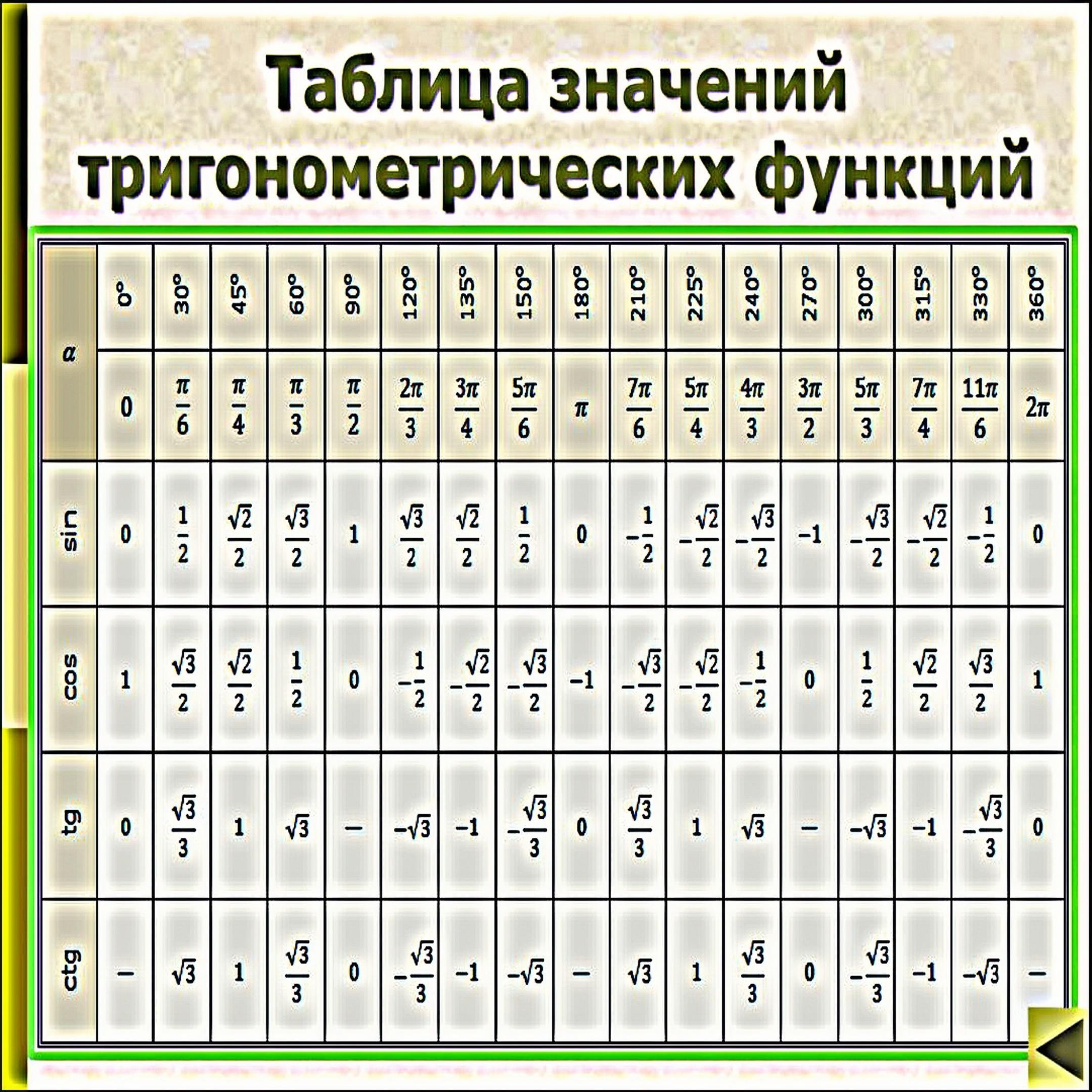
- Применим синус угла.
- Синус угла – отношение противолежащего катета к гипотенузе.
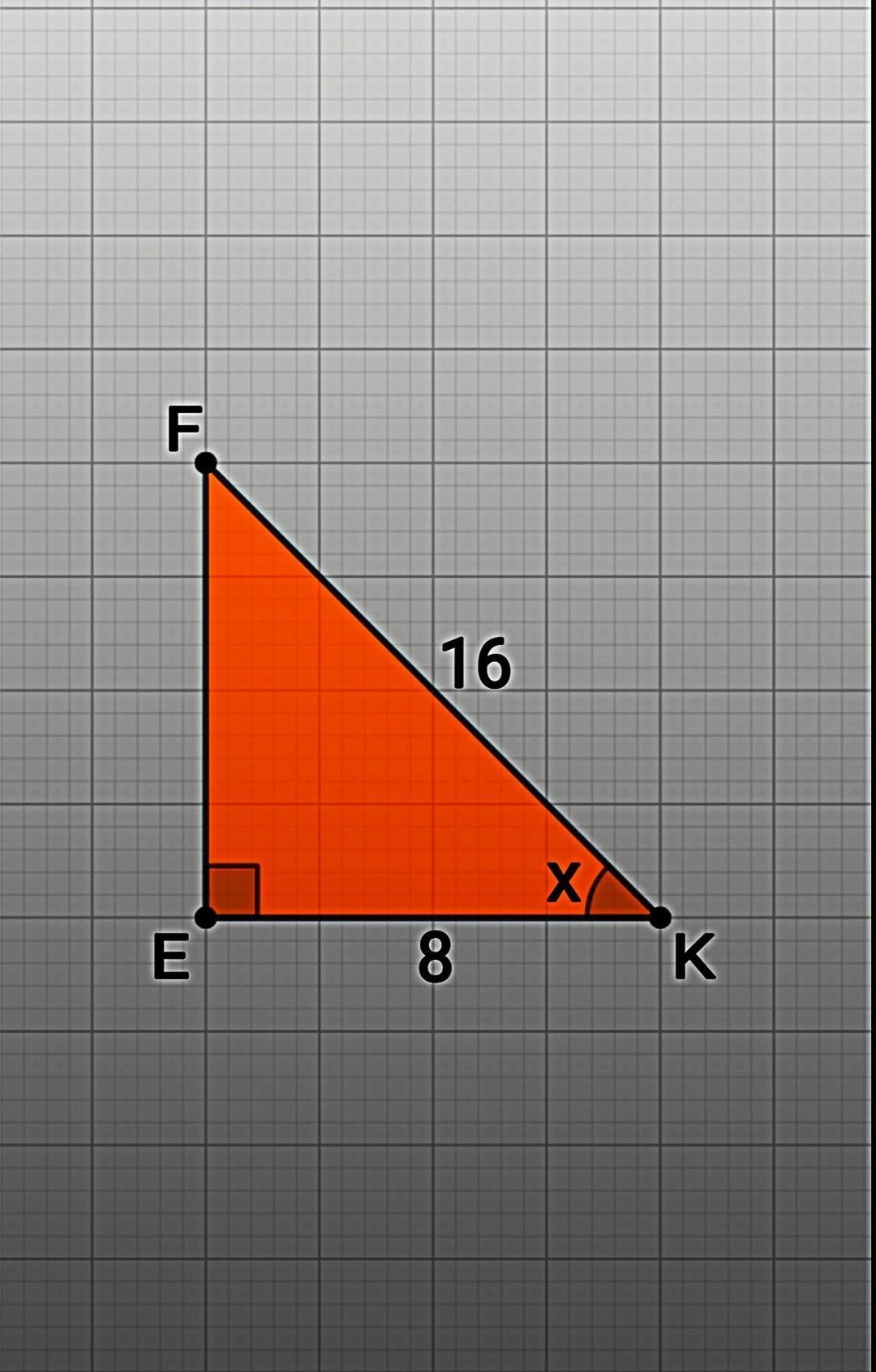
4)⠀Дано: FK =16см, ЕК = 8см, ∠Е = 90°
⠀⠀Найти: ∠х – ?
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение
- Такая же ситуация. Гипотенуза(FK) в 2 раза больше катета(EK). Следовательно ∠F = 30°.
- Сумма острых углов прямоугольного треугольника равна 90°. Тогда ∠х = 90° – 30° = 60°
Второй способ:
- Найдем неизвестный угол через косинус угла.
- Косинус угла – это отношение прилежащего катета к гипотенузе.
Доп. данные прикрепил вместе с чертежами.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ден715
Предмет: Русский язык,
автор: солнышкоячсфывйцу
Предмет: Английский язык,
автор: 5434567765432
Предмет: Русский язык,
автор: kamilla091110
Предмет: Математика,
автор: Munarashamshieva23