решите метод интервала срочно 50 баллов
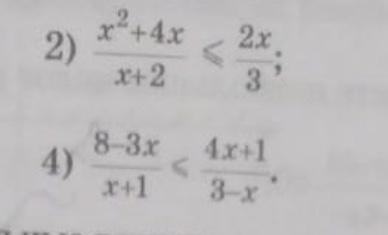
Ответы
Ответ:
2) х ∈ (-∞; 8) ∪ (-2; 0]
4) х ∈ (-23; -1] ∪ [1; 3)
Объяснение:
Решить методом интервалов:
2) Решим сначала уравнение:
Перенесем все влево. Приведем к общему знаменателю и найдем корни:
- Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю.
Получим точки:
х = 0; х = -8; х ≠ -2
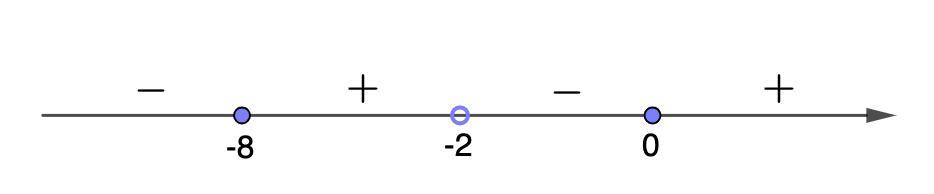
Отметим эти точки на числовой оси и найдем знаки нашего выражения на промежутках (см. рис). Причем точка (-2) будет выколотая.
1. x < -8.
Выбираем любую точку на промежутке, например, -10. Определим знак.
Первый множитель числителя будет отрицательным, второй тоже отрицательным и знаменатель будет отрицательным.
Тогда наша дробь будет иметь знаки:
2. -8 ≤ x < -2
Возьмем число (-5).
3. -2 < x ≤ 0
Возьмем (-1)
2. х ≥ 0
Подставим 1 и получим знак:
Так как у нас знак меньше или равно, то выбираем промежутки со знаком минус.
Получили ответ: х ∈ (-∞; 8) ∪ (-2; 0]
4) Решаем аналогично.
Разложим числитель на множители:
-х²+ х - 23х + 23 =х(1 - х) + 23(1 - х) = (1 - х)(х + 23)
Наше уравнение будет иметь вид:
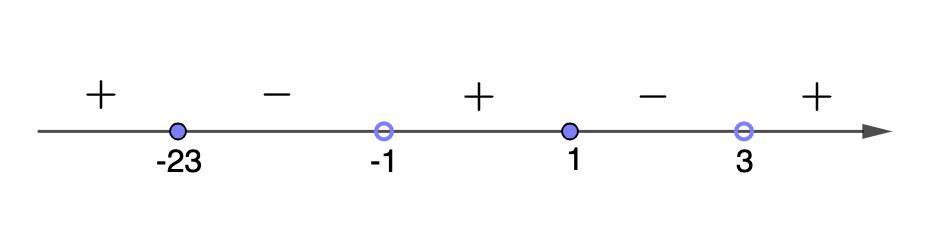
Отмечаем данные точки на числовой оси и определяем знаки на промежутках (см. рис)
Так как у нас знак меньше или равно, то выбираем промежутки со знаком минус.
Ответ: х ∈ (-23; -1] ∪ [1; 3)