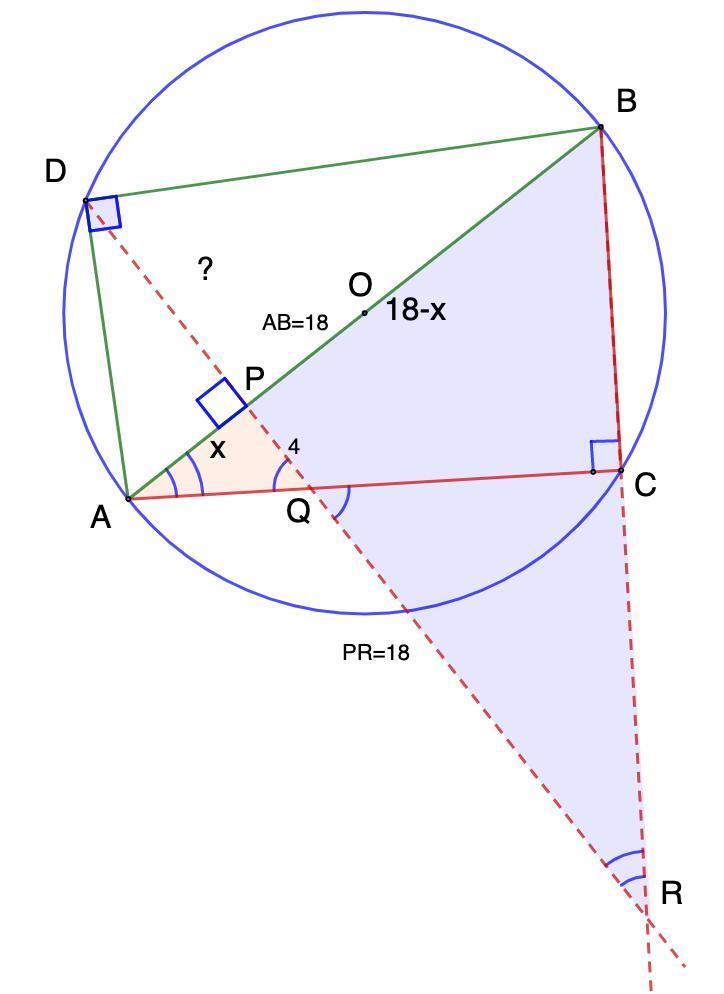
Треугольники ABC и ABD вписаны в одну и ту же окружность диаметра AB=18. Прямая, проходящая через D перпендикулярно AB, пересекает AB в точке P, сторону AC в точке Q и продолжение стороны BC в точке R.
Найдите длину DP, если PR=18 и PQ= 4.
Ответы
Ответ:
Длина DP равна 6√2 ед.
Пошаговое объяснение:
Треугольники ABC и ABD вписаны в одну и ту же окружность диаметра AB = 18. Прямая, проходящая через D перпендикулярно AB, пересекает AB в точке P, сторону AC в точке Q и продолжение стороны BC в точке R.
Найдите длину DP, если PR = 18 и PQ = 4.
Дано: Окр.О;
ΔABC и ΔABD - вписанные;
АВ - диаметр.
АВ = 18;
DR ⊥ AB; DR ∩ AB = P; DR ∩ AC = Q; DR ∩ BC = R;
PR = 18; PQ= 4.
Найти: PQ.
Решение:
- Вписанный угол, опирающийся на диаметр равен 90°.
⇒ ΔABC и ΔABD - прямоугольные.
1. Рассмотрим ΔAPQ и ΔQCR - прямоугольные.
- Вертикальные углы равны.
⇒ ∠AQP = ∠RQC (вертикальные)
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠PAQ = 90° - ∠AQP
∠QRC = 90° - ∠RQC
⇒ ∠PAQ = ∠QRC
2. Рассмотрим ΔAPQ и ΔRPB - прямоугольные.
∠PAQ = ∠QRC (п.1)
⇒ ΔAPQ ~ ΔRPB (по двум углам)
Пусть АР = х; тогда РВ = (18 - х)
Составим отношения сходственных сторон.
Если АР = 12, то РВ = 18 - 12 = 6
Если АР = 6, то РВ = 18 - 6 = 12
Для нашего рисунка удобней применить второй вариант:
АР = 6, РВ = 12.
3. Рассмотрим ΔADB - прямоугольный.
DP - высота.
- Квадрат высоты прямоугольного треугольника, проведённой к гипотенузе, равен произведению проекций катетов на гипотенузу.
⇒ BD² = AP · PB = 6 · 12 = 72
BD = √72 = 6√2
Длина DP равна 6√2 ед.
#SPJ1