Question

Помогите решить неравенство

Answer 1

Ответ:

$x \in \left( {\frac{1}{2};\,\,1} \right) \cup [2;\,\, + \infty )$

Пошаговое объяснение:

ОДЗ:

$\left\{ \begin{array}{l}2x - 1 > 0,\\4x > 0,\\4x \ne 1,\\2x - 1 \ne 1;\end{array} \right.\\\\\left\{ \begin{array}{l}x > \displaystyle\frac{1}{2},\\x > 0,\\x \ne \displaystyle\frac{1}{4},\\x \ne 1;\end{array} \right.\\\\x \in \left( {\displaystyle\frac{1}{2};\,\,1} \right) \cup (1;\,\, + \infty ).$

Первая скобка превращается в ноль при

${4^{ - \displaystyle\frac{1}{x}}} = 16;\\\\{4^{ - \displaystyle\frac{1}{x}}} = {4^2};\\\\ - \displaystyle\frac{1}{x} = 2;\\\\x = - \displaystyle\frac{1}{2}.$

Вся ОДЗ лежит правее найденного значения, поэтому знак этой скобки на ОДЗ всегда одинаков. Например, при $x = 2$ ее значение

${4^{ - \displaystyle\frac{1}{2}}} - 16 = \displaystyle\frac{1}{{\sqrt 4 }} - 16 < 0.$

С учетом этого неравенство можно упростить:

$\displaystyle\frac{{x - 2}}{{{{\log }_{4x}}(2x - 1)}} \ge 0.$

$x-2$ превращается в ноль при $x = 2$.

Знаменатель превращается в ноль, когда

${\log _{4x}}(2x - 1) = {\log _{4x}}1;\\\\2x - 1 = 1;\\\\2x = 2;\\\\x = 1.$

Так как $4x > 1$ на ОДЗ, то проверкой убеждаемся, что ${\log _{4x}}(2x - 1) < 0$ при $x \in \left( {\displaystyle\frac{1}{2};\,\,1} \right)$ и ${\log _{4x}}(2x - 1) > 0$ при $x \in (1;\,\, + \infty ).$

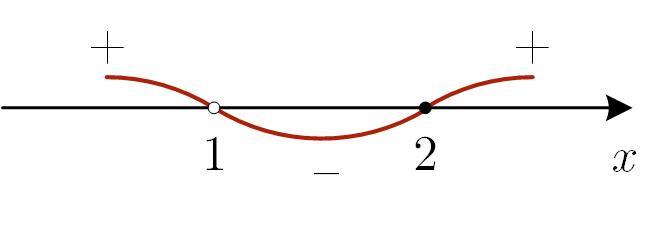
С помощью метода интервалов определяем знаки неравенства на промежутках знакопостоянства (см. рис.).

Учитывая ОДЗ, получаем: $x \in \left( {\displaystyle\frac{1}{2};\,\,1} \right) \cup [2;\,\, + \infty ).$