Question

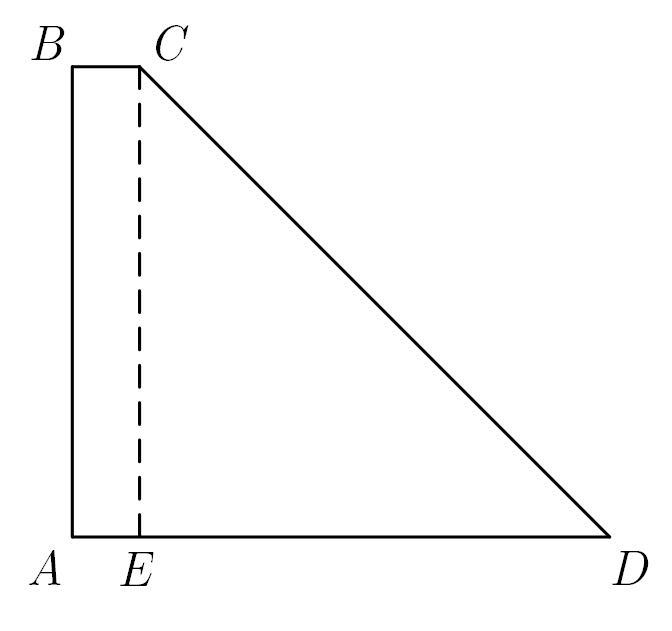
у прямокутній трапеції ABCD з прямим кутом A основи BC i AD відносяться як 1:8. кут BCD = 135 градусів, середня лінія MN = 18 см. Знайти менше бічну сторону трапеції

Answer 1

Ответ:

$AB = 28$

Объяснение:

Пусть $BC = x$, $AD = 8x$, тогда средняя линия

$MN = \displaystyle\frac{{AB + CD}}{2} = \displaystyle\frac{{x + 8x}}{2} = 18;\\\\9x = 36;\\\\x = 4.$

Так как $\angle BCD = 135^\circ$, а сумма углов при боковой стороне трапеции равна $180^\circ$, то $\angle ADC = 180^\circ - 135^\circ = 45^\circ .$

Опустим высоту из вершины $C$. Тогда прямоугольный треугольник $CED$ — равнобедренный.

$AB = CE = DE = AD - AE = AD - BC = 8x - x = 7x = 7 \cdot 4 = 28.$