Решите уравнение
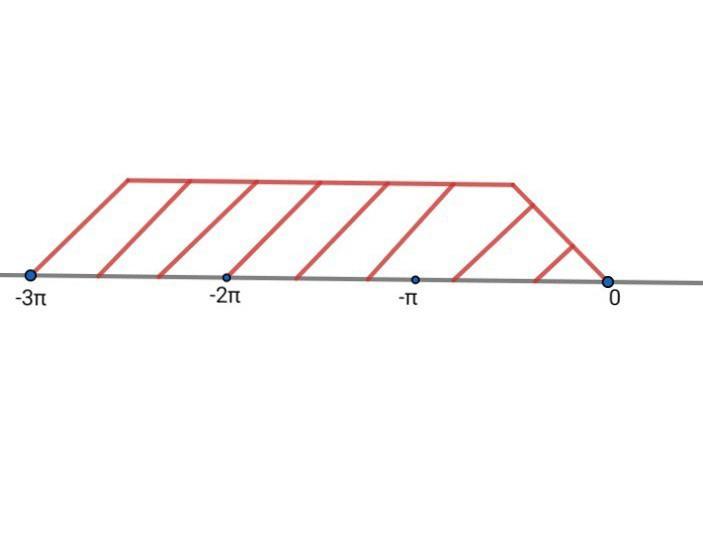
Укажите корни на отрезке
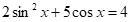
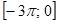
Ответы
Відповідь:
Покрокове пояснення:
2sin²x + 5cosx = 4 ; xЄ [- 3π ; 0 ] ;
2( 1 - cos²x ) + 5cosx - 4 = 0 ;
2 - 2cos²x + 5cosx - 4 = 0 ;
- 2cos²x + 5cosx - 2 = 0 ;
2cos²x - 5cosx + 2 = 0 ;
введемо нову змінну t = cosx , ( | t | ≤ 1 ) :
2t² - 5t + 2 = 0 ;
D = 25 - 16 = 9 > 0 ; t = 1/2 ; t = 2 > 1 .
Повернемося до змінної х :
cosx = 1/2 ;
x = ± π/3 + 2πn , nЄ Z . Відберемо корені з проміжка :
x = - π/3 ; x = - 1 2/3 π ; x = - 2 1/3 π .
Ответ:
Пошаговое объяснение:
Согласно основному тригонометрическому тождеству заменим , 4 перенесём к левой части и все это приравним к нулю:
Раскроем скобки:
2 и -4 подобные , а с cos x сделаем замену , тогда cos x = t:
Если перед уравнением стоит отрицательный знак , то все знаки уравнения меняются на противоположный , распишем по порядку квадратного уравнения , исходя из вида ax²±bx±c=0:
Укажем коэффициенты данного уравнения и найдём дискриминант по формуле: b²-4ac:
D>0 , значит данное уравнение будет иметь два корня , а их найдем по формуле:
Сделаем обратную замену t = cos x , где :
Косинус принимает промежуток от -1 до 1 , 2>1 , значит cosx=2∉R , а cosx= принажлежит к данному промежутку и на единичной окружности имеет следущие значения:
n - это целое число , в эти корни мы должны подставить такие целые числа , при котором будут удовлетворять неравенство или же корень должен принадлежать к промежутку
, но в наш промежуток должны входить отрицательные корни , т.к промежуток находится слева от нуля , значит
;тогда
Подставим поочередно наши n - рассмотрев первый корень:
При n= -1 : , корни которые будут входить в промежуток [-3π ; 0] будут со знаменятелями 3 , достаточно - просто увериться , что x≥-3π , тогда для удобства превратим -3π в дробь , которая будет со знаменателем 3 , это :
, тут же можно удобно сравнить -5π/3 и -9π/3 дроби с одинаковыми знаменателями , сравниваются только числители -5π>-9π , если x больше , тогда корень входит в промежуток [-3π ; 0] .
При n= -2 : , -11π/3<-9π/3 ⇔-11π<-9π , не входит в промежуток [-3π ; 0] , анологично , что при n=-3,-4,-5... тоже не будет входить в промежуток [-3π ; 0] .
Тогда , рассмотрим при отрицательных n :
При n= -1 : , -π/3>-9π/3 ⇔ -π>-9π , входит в промежуток [-3π ; 0]
При n= -2 : , -7π/3>-9π/3 ⇔ -7π>-9π , входит в промежуток [-3π ; 0]
При n= -3 : , -13π/3<-9π/3 ⇔ -13π<-9π , не входит в промежуток [-3π ; 0] , также анологично , что при n= -4,-5 ,-6... тоже не будет входить в промежуток .