Предмет: Алгебра,
автор: jobmainac
Помогите пожайлуста решить эту задачу
Приложения:
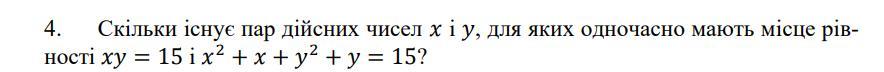
Ответы
Автор ответа:
0
Ответ:
Не существует ни одной пары чисел, удовлетворяющих условию задачи
Объяснение:
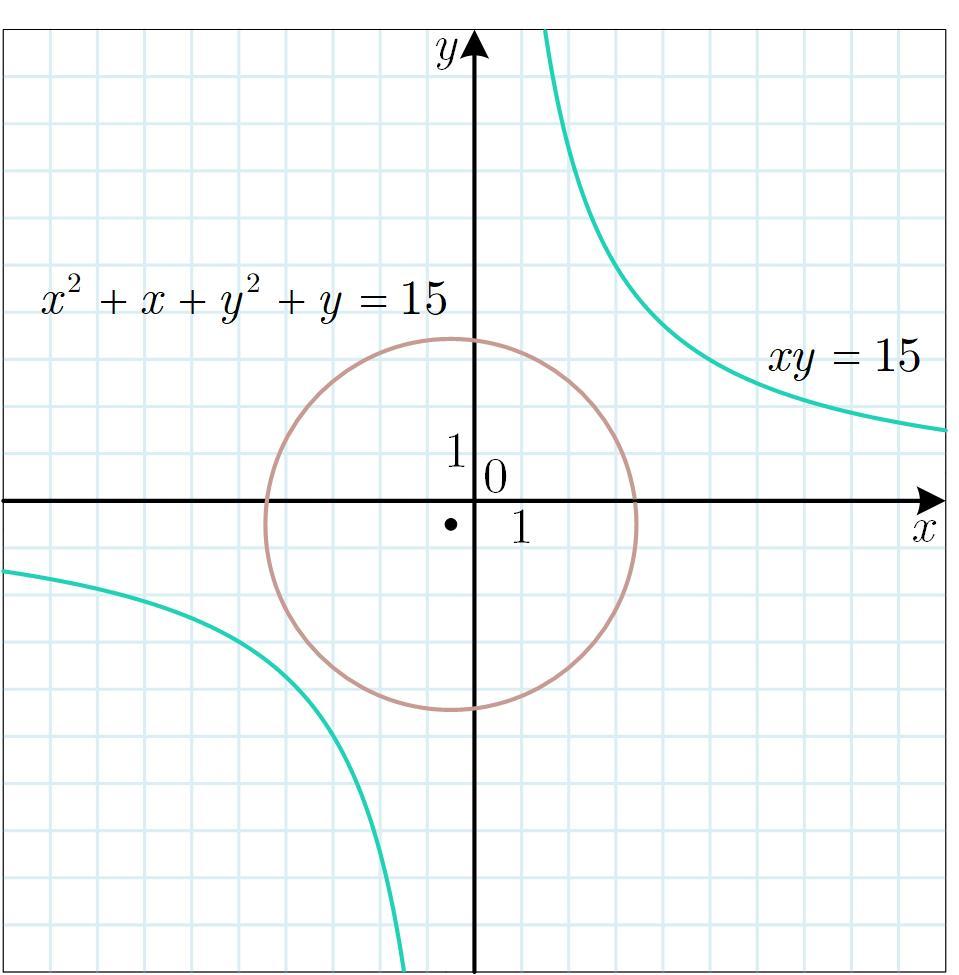
Первое уравнение задает гиперболу
а второе уравнение — окружность:
с центром и радиусом
Изобразим оба графика в одной координатной плоскости (см. рис).
Кривые не пересеклись, значит таких пар действительных чисел не существует.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: RLR1
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: поаагпгщои
Предмет: Алгебра,
автор: likaln437
Предмет: Геометрия,
автор: stas2437