Предмет: Алгебра,
автор: jobmainac
ПРОШУ, ПОМОГИТЕ с задание на фото
Приложения:
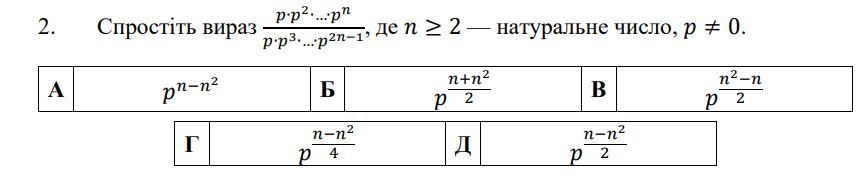
Ответы
Автор ответа:
0
Ответ:
Д)
Объяснение:
Так как
выражение можно переписать
Сумма — арифметическая прогрессия с
,
и количеством членов, равным
. Тогда
Сумма — арифметическая прогрессия с
,
и количеством членов, равным
. Тогда
Значит
tamarabernukho:
...
https://ibb.co/x8sNdxj
Упс :(
Похожие вопросы
Предмет: Қазақ тiлi,
автор: anastasiagloba9
Предмет: Английский язык,
автор: филя24
Предмет: Русский язык,
автор: КанинаПолина
Предмет: Английский язык,
автор: benedictcamber
Предмет: Математика,
автор: Аноним